
Discrete Phase Model (DPM): Drag Law
Introduction
This article discusses all drag law models provided in ANSYS Fluent software. There are 14 models available. It has been tried to investigate the most applicable models.
Drag Law Models
Totally, there are fourteen drag law models available in ANSYS Fluent software. Four are always available, and the rest require specific conditions.
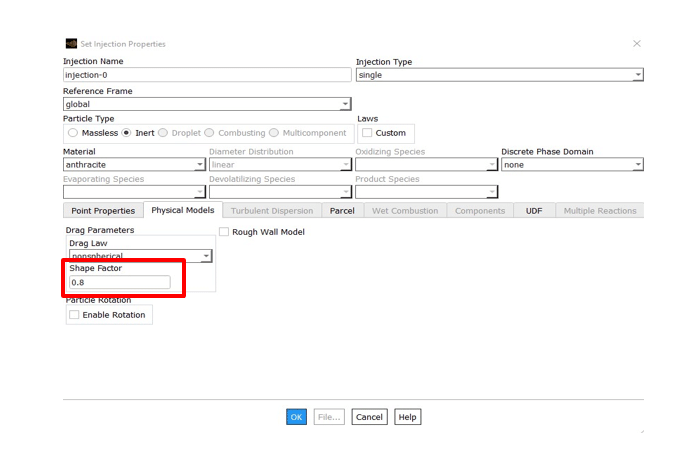
Injection —–> Physical Models ——> Drag Law
- Spherical
- Nonspherical
- Stokes-Cunningham
- High-Mach-Number
- Dynamic-Drag
- Wen-Yu
- Gidaspow
- Huilin-Gidaspow
- Syamlal-OBrien
- Gibilaro
- EMMS
- Filtered Two-fluid Model (TFM)
- Ishii-Zuber
- Grace
1) Spherical Particles
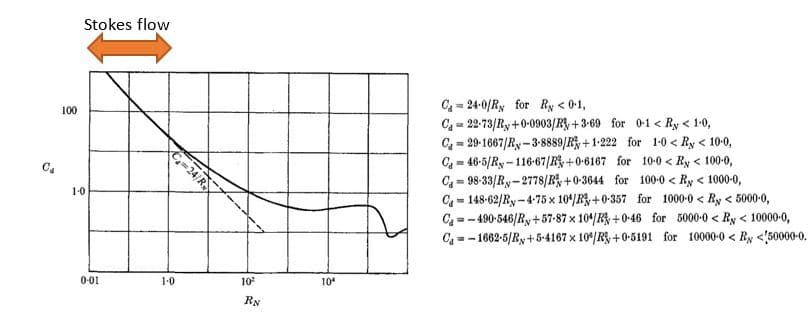
As its name indicates, the particles are assumed as smooth spheres. The Morsi-Alexander relationship selected the spherical particle model to apply drag effects to discrete phase problems. This relationship was derived from experimental results. There are three constants; by changing the amplitude of the particle Reynolds number and fitting the experimental curve, obtained an equation of the following form:
2) Non-Spherical Particles
The developed Haider and Levenspiel model applies drag force to non-spherical but uniform particles. According to the spherical state, an analytical relation to the experimental data was fitted in this model. The proposed relationship with different coefficients was as follows:
The coefficient in the above relation was defined as follows and named the shape factor. An example displayed the shape factor of a cubic particle to understand the effect of this coefficient better.
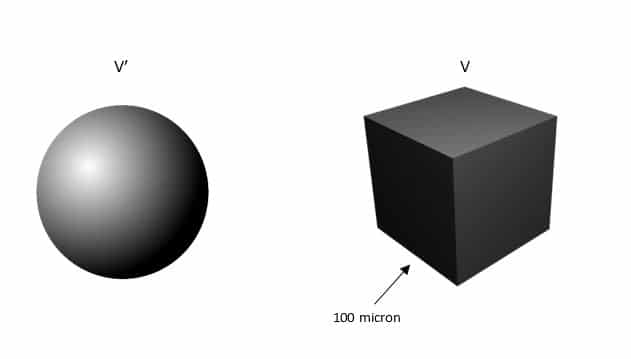
The ratio is the surface area of a sphere with a volume equal to the volume of the non-spherical particle to the area of the actual surface of the non-spherical particle.
The above calculations indicate the diameter of the non-spherical particle equivalent to the spherical state. So the value of the shape factor for the cube particle state was 0.8. In the following animation, a spherical and a non-spherical particle is falling.
3) Stokes-Cunningham
This drag model is used for particles with sub-micron sizes (D<1µm). The Stokes form of drag law is developed as follows:
In the above relation is the drag coefficient and
is the Cunningham correction to Stokes’ drag law[3].
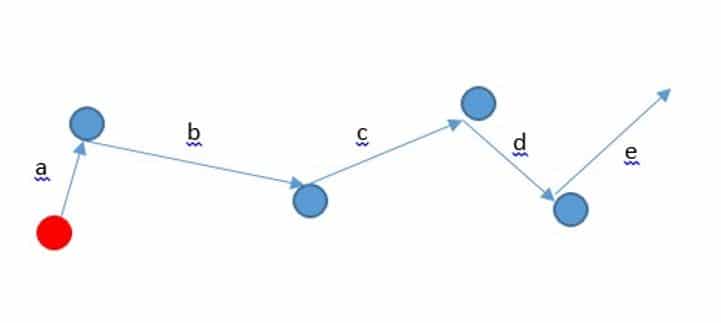
Also, is the molecular mean free path. The following equation is used to obtain the molecular mean free path.
4) High-Mach-number
This model uses the same drag force defined as the spherical, but a correction factor is added. This model is used for the Mach number of particles greater than 0.4 or Reynolds number of particles greater than 20.
5) Dynamic-drag
This model is only available when the droplet break-up model is enabled. In the spraying process, the droplets are distorted and their shape doesn’t remain spherical. On the other hand, the drag coefficient strongly depends on droplet shape. The droplet’s shape changes to a disk-shaped during movement, so it has higher drag compared to a sphere droplet. Thus, the following relation is defined:
Y is the droplet distortion. According to the relation, when there isn’t any distortion (Y=0), the drag coefficient of a spherical droplet will be obtained, while at the maximum distortion (Y=1), the drag coefficient gets higher.
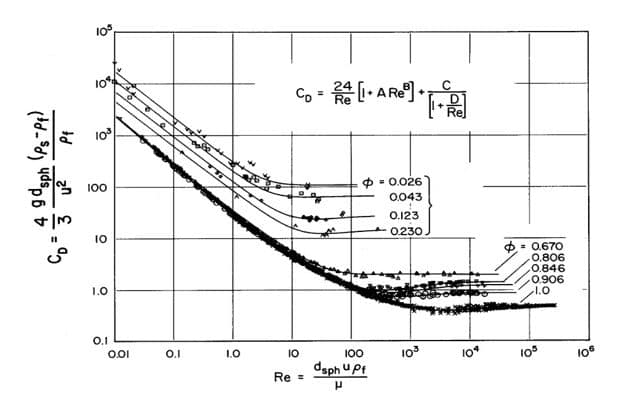
6-12) Wen-Yu, Gidaspow, Huilin-Gidaspow, Syamlal-Obrien, Gibilaro, EMMS and Filtered two-fluid model (TFM)
*** There are 7 drag law models which are available when the Dense Discrete Phase Model (DDPM) is enabled, including Wen-Yu, Gidaspow, Huilin-Gidaspow, Syamlal-Obrien, Gibilaro, EMMS and Filtered two-fluid model (TFM).
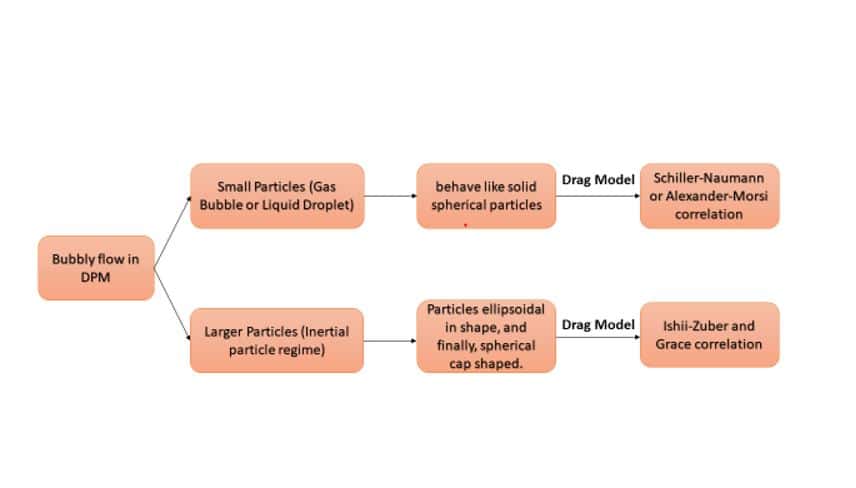
13-14) Ishii-Zuber, Grace
The Ishii-Zuber and Grace drag law models are available when applying the gravitational vector. Plus, we use the model in gas-liquid flows simulations.
In the viscous Regime, bubbles and discrete droplets behave as spherical solid particles, so we can use the model of Alexander-Morsi to investigate the drag force.
The drag coefficient is not dependent on the Reynolds number and has an approximately constant value but is partially dependent on the Eotvos dimensionless number.
In the above relation is the acceleration of gravity,
the density difference between the phases, and the surface tension coefficient.
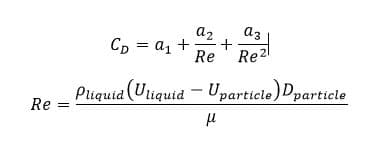

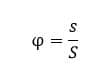
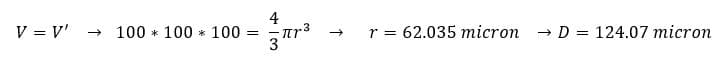
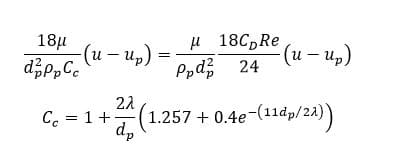
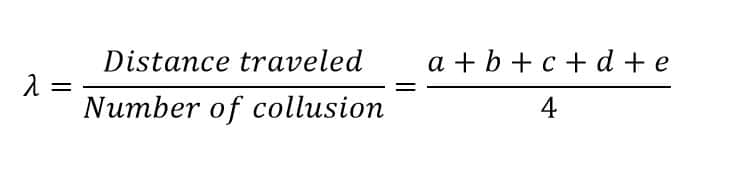

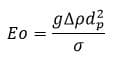



Comments (0)