Dynamic Stability Derivatives for Javelin Rocket CFD Simulation, ANSYS Fluent

Description

Description

This project aims to obtain dynamic stability derivatives for the Javelin rocket, a shoulder-fired, unguided, rocket-propelled missile designed for portability and ease of use by individual soldiers in combat situations. Due to the absence of horizontal and vertical stabilizers, conventional methods for calculating derivatives and conducting stability analysis may not be straightforward for this unconventional configuration.

we employ ANSYS Fluent software and leverage the applications of Computational Fluid Dynamics (CFD) in flight dynamics to obtain the necessary derivatives. In this simulation, we developed a User-Defined Function (UDF) file to accurately model the Javelin rocket’s motion during flight.

The Javelin rocket is designed to fly in a Mach number of 1.7 at sea level altitude. The geometry of the Javelin rocket is meticulously designed using SpaceClaim software, ensuring high fidelity to the actual Rocket. To discretize the computational domain, an unstructured mesh grid is generated using ANSYS Meshing software. The resulting mesh consists of 4,245,614 cells, providing a detailed representation of the flow field around the Javelin rocket.

You can Also view the aerodynamic and  Dynamic Mesh simulation of this product

Methodology

To simulate the Javelin rocket’s motion, we employ mesh motion techniques and UDF files. The simulation is set up with a velocity of 1.7 Mach and an operating pressure of 101,325 Pa, representing sea-level conditions. The simulation begins with the Javelin rocket at a zero-degree angle of attack, and a forced oscillation motion is modeled to capture the dynamic stability characteristics. The UDF file is programmed to prescribe the desired motion of the Javelin rocket, including pitch, yaw, and roll oscillations.

The simulation employs the Realizable K-ε turbulence model, to capture the complex flow phenomena around the Javelin rocket. The CFD solver is configured to resolve the boundary layer accurately, capture flow separation, and predict the aerodynamic forces and moments acting on the rocket.

Results

Post-processing the simulation results involves extracting the relevant aerodynamic coefficients, such as lift, drag, and moment coefficients, at each time step. These coefficients are then analyzed to determine the dynamic stability derivatives, including pitch damping (Cmq), yaw damping (Cnr), roll damping (C_lp), and lift force derivative (CLα).

The obtained dynamic stability derivatives provide valuable insights into the Javelin rocket’s stability and control characteristics.

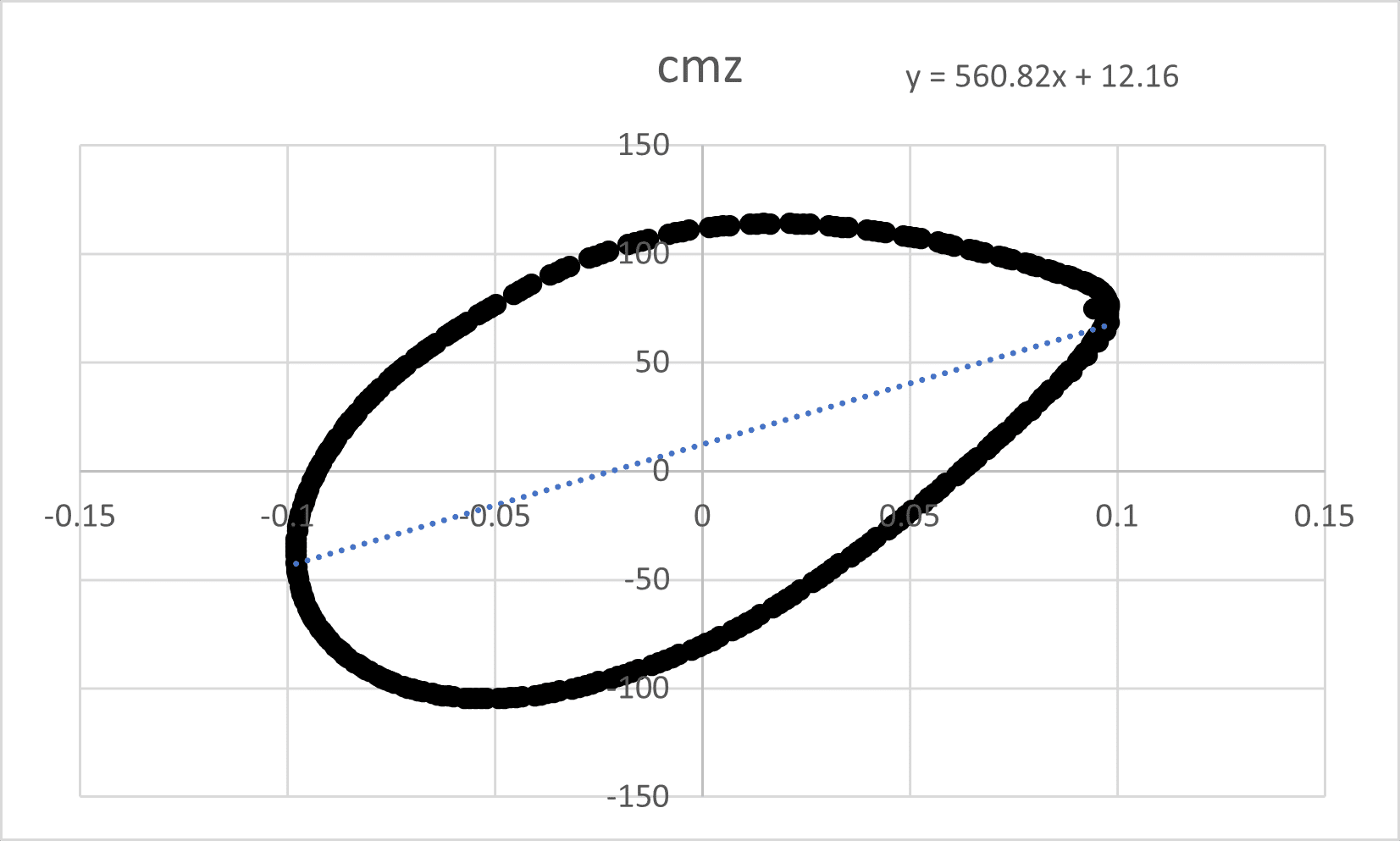
C_mz (Moment Coefficient about the Z-axis):

The equation y = 560.82x + 12.16 shows a strong positive relationship between cmz and the motion variable (likely the yaw rate).

The large positive slope (560.82) suggests a significant positive yaw damping derivative (Cnr), which is beneficial for yaw stability.

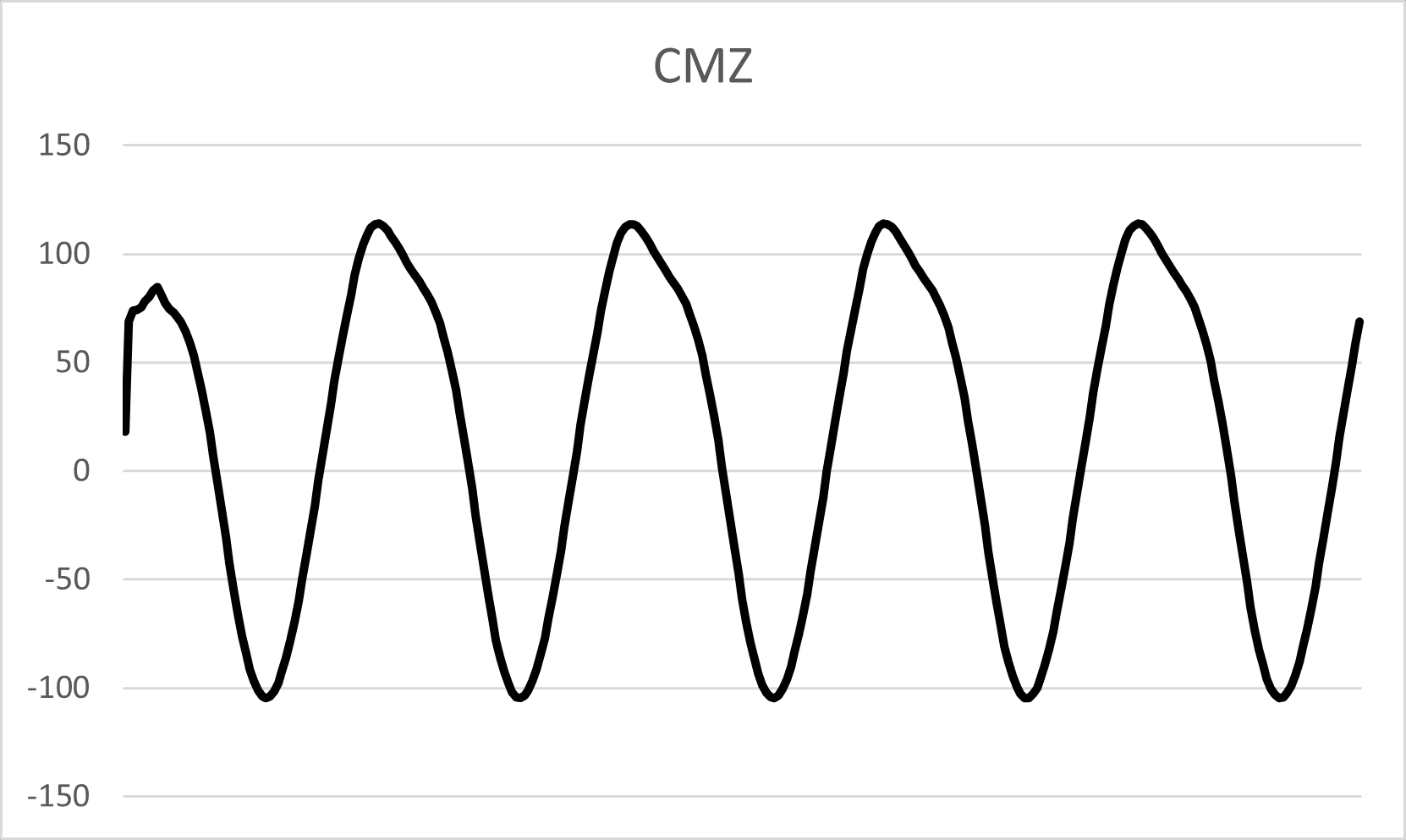
The periodic oscillations in Cmz overflow time indicate the presence of a yaw-damping moment that helps stabilize the rocket’s yawing motion.

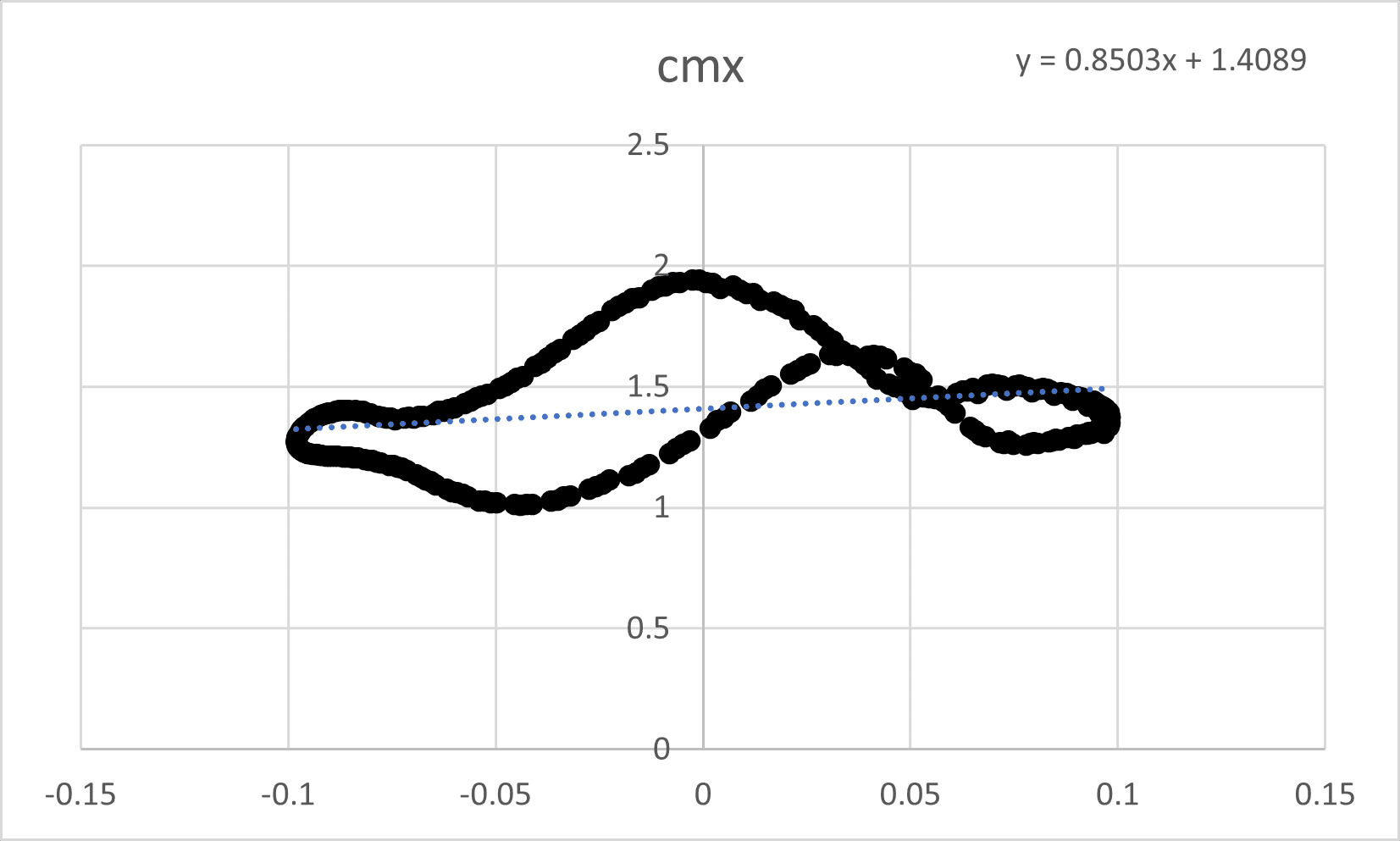
Cmx (Moment Coefficient about the X-axis):

The equation y = 0.8503x + 1.4089 suggests a positive relationship between C_mx and the motion variable (likely the pitch rate).

The positive slope (0.8503) indicates a positive pitch damping derivative (C_mq), which is desirable for pitch stability.

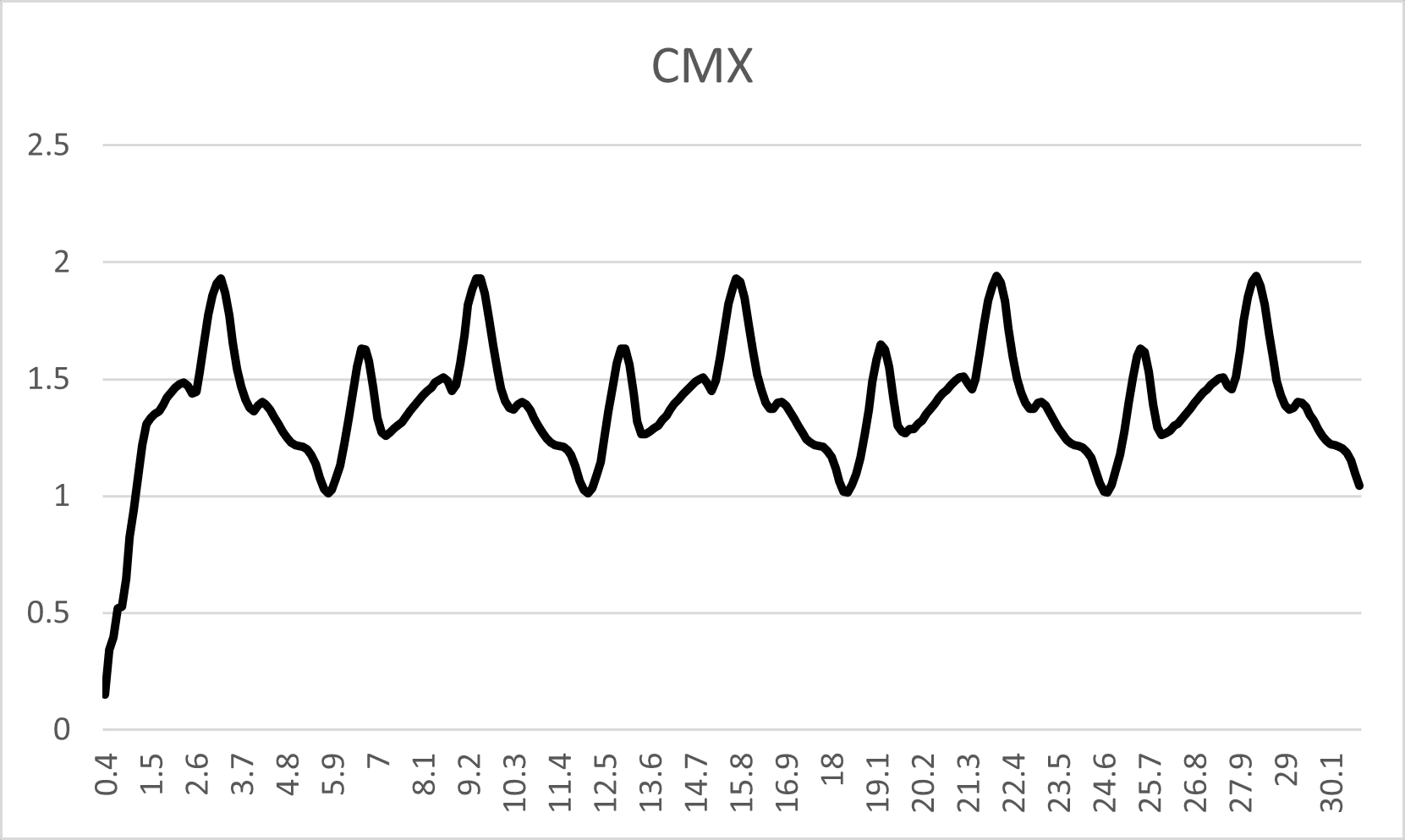
The periodic oscillations in C_mx overflow time suggest the presence of a pitch-damping moment that helps stabilize the rocket’s pitching motion.

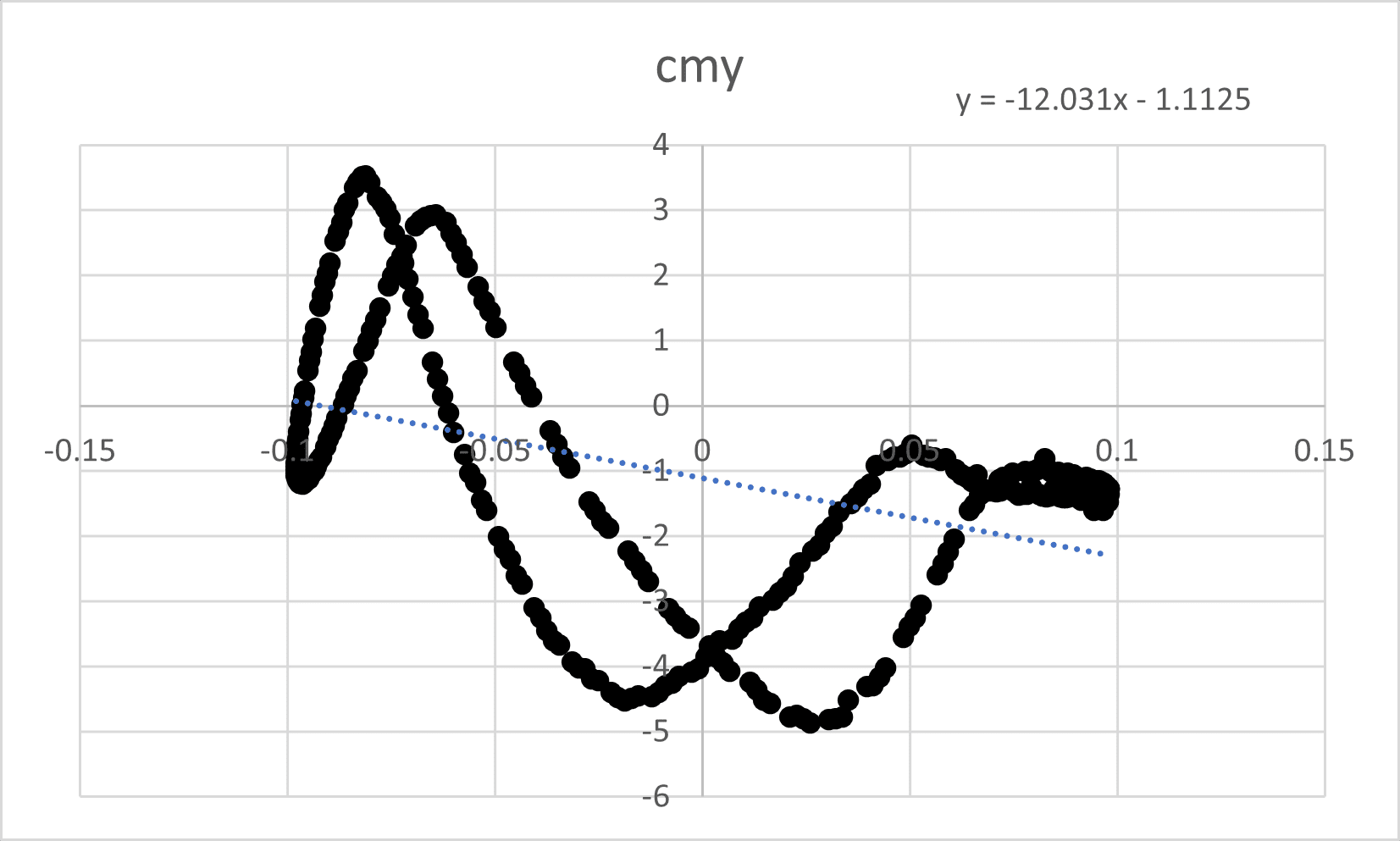
C_my (Moment Coefficient about the Y-axis):

The equation y = -12.031x – 1.1125 indicates a negative relationship between C_my and the motion variable (likely the pitch rate).

The negative slope (-12.031) suggests a negative pitch damping derivative (Cmq) about the Y-axis.

The oscillations in C_my overflow time are in phase with Cmx, indicating a coupling between the pitching moments about the X and Y axes.

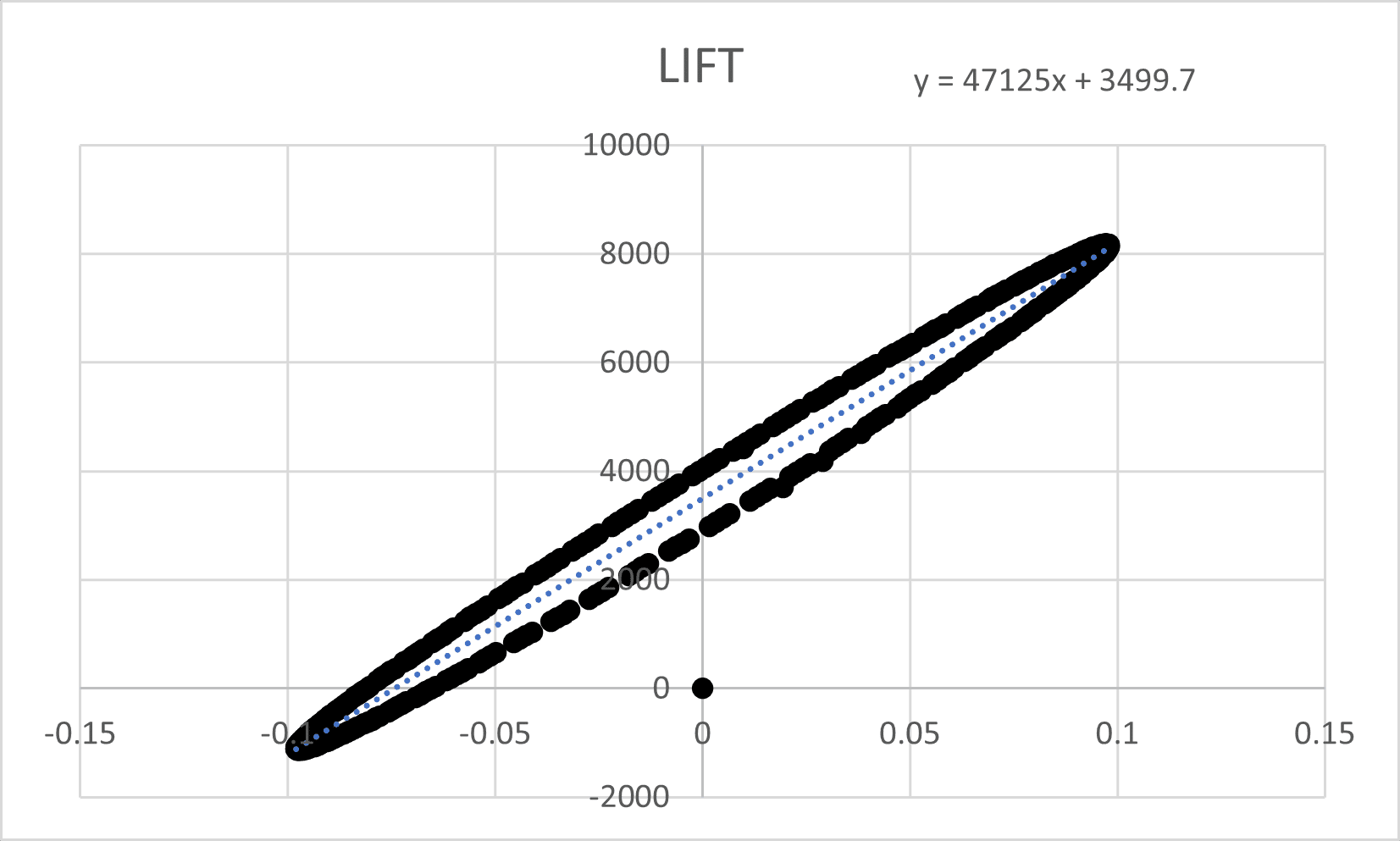
Lift (Lift Coefficient):

The equation y = 0.1354x + 0.0101 demonstrates a strong positive relationship between the lift coefficient and the motion variable (likely the angle of attack).

The positive slope (0.1354) suggests lift force derivative (CLα), indicating that the rocket generates significant lift force as the angle of attack increases.

The periodic oscillations in lift-over over time are in phase with C_mx and C_my, suggesting a coupling between the lift force and the pitching moments.

Overall, the provided dynamic stability derivatives seem to be reasonable and consistent with the observed behavior of the Javelin rocket in the simulation. The positive pitch damping (Cmq) about the X-axis, negative pitch damping (Cmq) about the Y-axis, and positive yaw damping (Cnr) contribute to the stability of the rocket’s pitching and yawing motions

However, it’s important to validate these derivatives against experimental data or theoretical predictions to ensure their accuracy. Additionally, further analysis of the coupling between the aerodynamic coefficients and the motion variables can provide deeper insights into the rocket’s dynamic stability characteristics.

By leveraging the power of CFD simulations and the ANSYS Fluent software suite, this project aims to provide a comprehensive understanding of the Javelin rocket’s dynamic stability, enabling engineers to make informed design decisions and ensure the aircraft’s safe and efficient operation.