Electric Field Effect on Nanofluid Heat Transfer (EHD)
$210.00 $105.00 Student Discount
In this project, nanofluid flows in a bumpy channel in presence of an applied electrical potential.
Click on Add To Cart and obtain the Geometry file, Mesh file, and a Comprehensive ANSYS Fluent Training Video.To Order Your Project or benefit from a CFD consultation, contact our experts via email (info@mr-cfd.com), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via info@mr-cfd.com after you buy the product.
Description
Electric Field Effect on Nanofluid Heat Transfer (EHD), ANSYS Fluent CFD Simulation Training
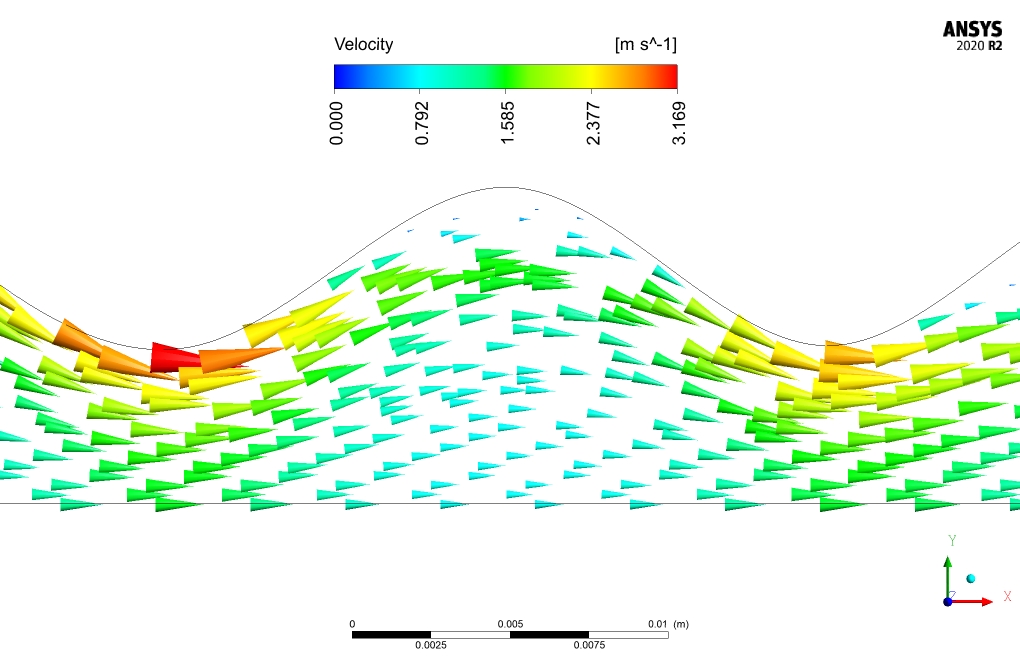
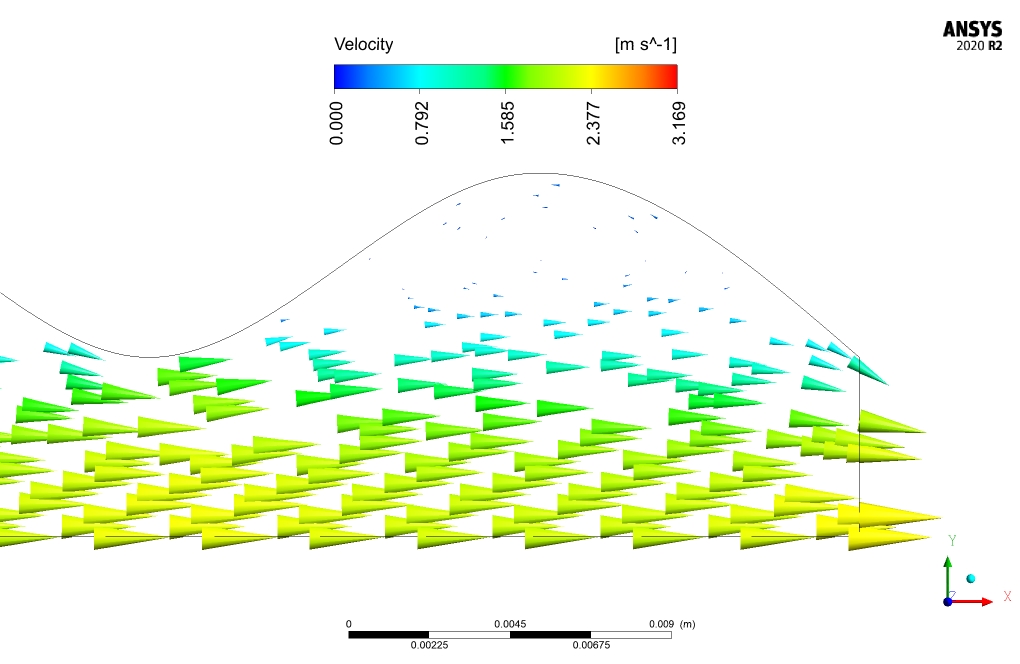
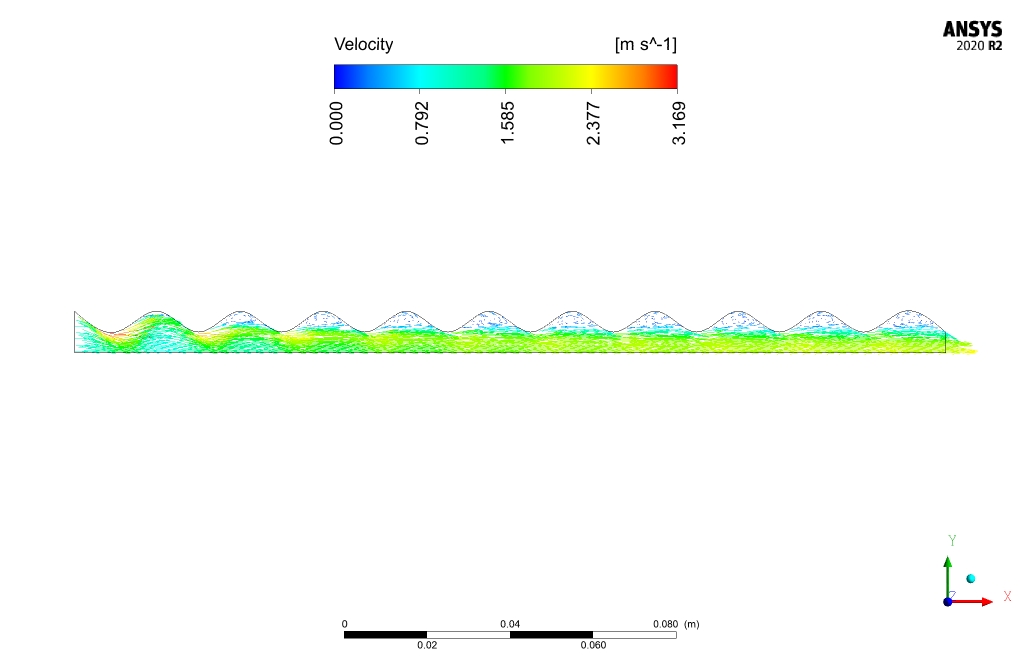
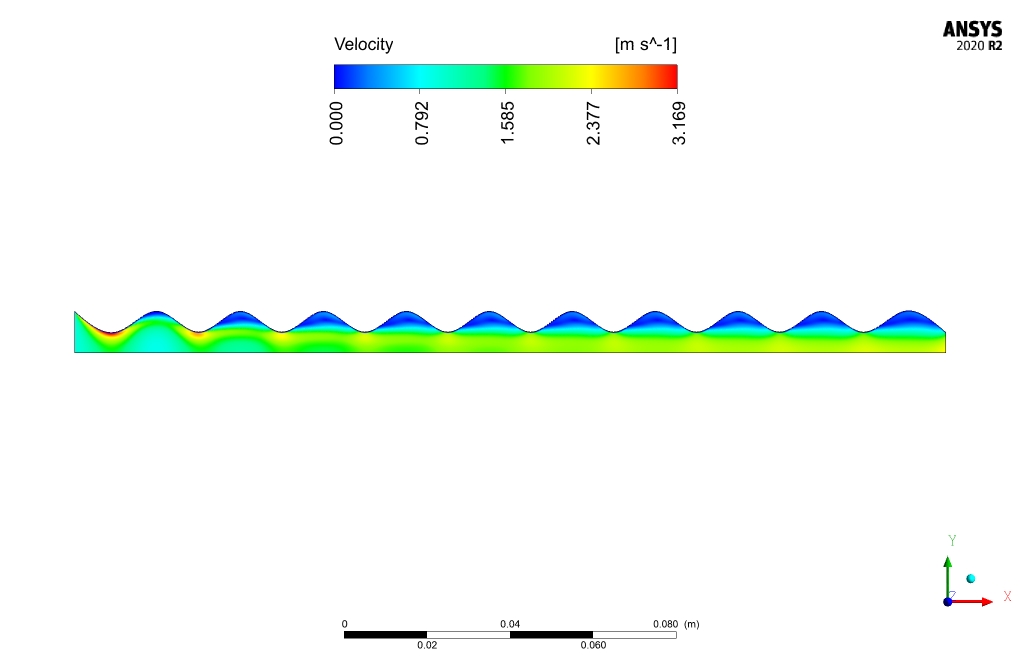
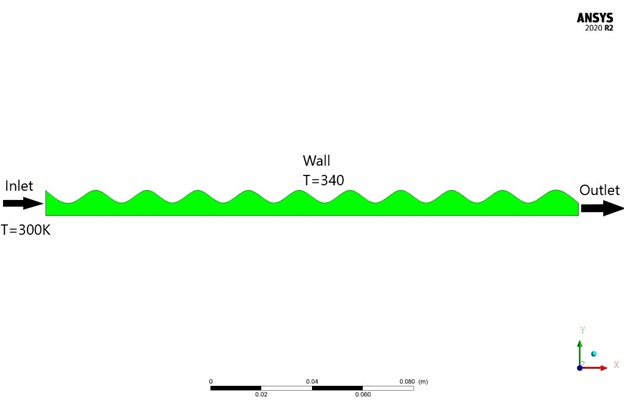
In this project, nanofluid flows in a bumpy channel in the presence of an applied electrical potential applying ANSYS Fluent software. Fluid flow is steady and is simulated as one single-phase flow, however, the thermophysical properties of nanofluid are modified. The electrical characteristics of nanofluid alter the fluid mechanics behavior of flow which results in heat transfer increase. The surface average of the nanofluid’s temperature is equal to 300 and 301.926K at the inlet and outlet respectively.
where are density, viscosity, specific heat, and thermal conductivity coefficient of nano-fluid and volume fraction of nanoparticles in fluid.
Geometry and mesh
The geometry of the fluid domain is designed in the Design modeler and the computational grid is generated using Ansys Meshing. The mesh type is unstructured and the element number is 17640.
Electric Field CFD Simulation
Critical assumptions:
- The solver type is assumed Pressure Based.
- Time formulation is assumed Steady.
- Gravity effects are neglected.
The following table is a summary of the defining steps of the problem and its solution.
| Models (electric field) | ||
| Energy | On | |
| Viscous | K-epsilon (realizable) | Standard wall function |
| Materials | ||
| Fluid | Definition method | Fluent Database |
| Material name | Water (modified) | |
| Density | 998.2 kg/m3 | |
| Specific heat (Cp) | 4182 J/kg.K | |
| Thermal conductivity | 0.6 w/m.K | |
| Viscosity | 0.001003 kg/m.s | |
| UDS diffusivity | constant | |
| Electrical conductivity | 1000000 siemens/m | |
| Magnetic permeability | 1.257e-6 | |
| Cell zone conditions | ||
| Fluid | Material name | Water (modified) |
| Boundary conditions (electric field) | ||
| Inlet | Type | Velocity inlet |
| Velocity magnitude | 1 m/s | |
| Turbulence intensity | 5% | |
| Turbulent viscosity ratio | 10 | |
| Temperature | 300 K | |
| Outer Wall solid | Temperature | 340 K |
| Solver configurations | ||
| Pressure-velocity coupling | Scheme | SIMPLE |
| Spatial discretization | Gradient | Least square cell-based |
| Pressure | Second order | |
| Momentum | Second order Upwind | |
| Turbulent kinetic energy | First order upwind | |
| Turbulent dissipation rate | First order upwind | |
| Energy | Second order Upwind | |
| Initialization (electric field) | Method | Hybrid |
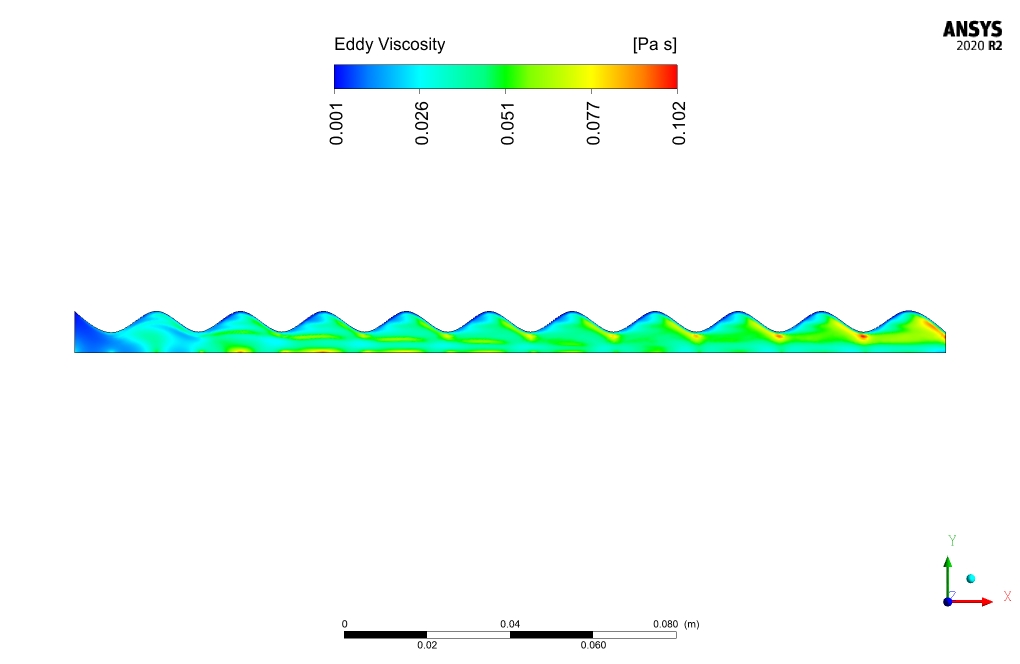
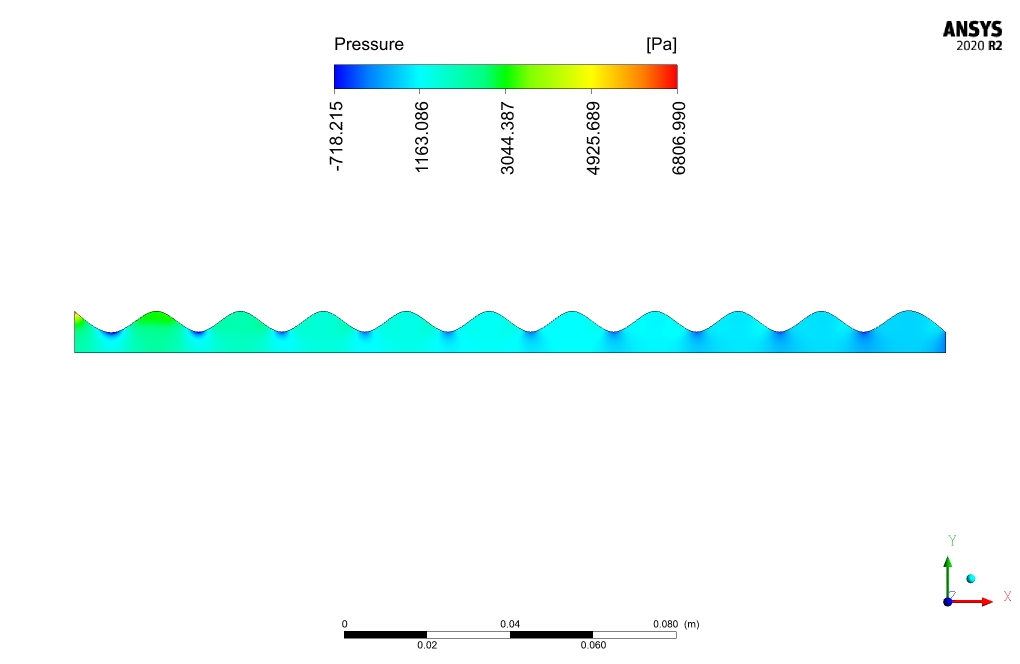
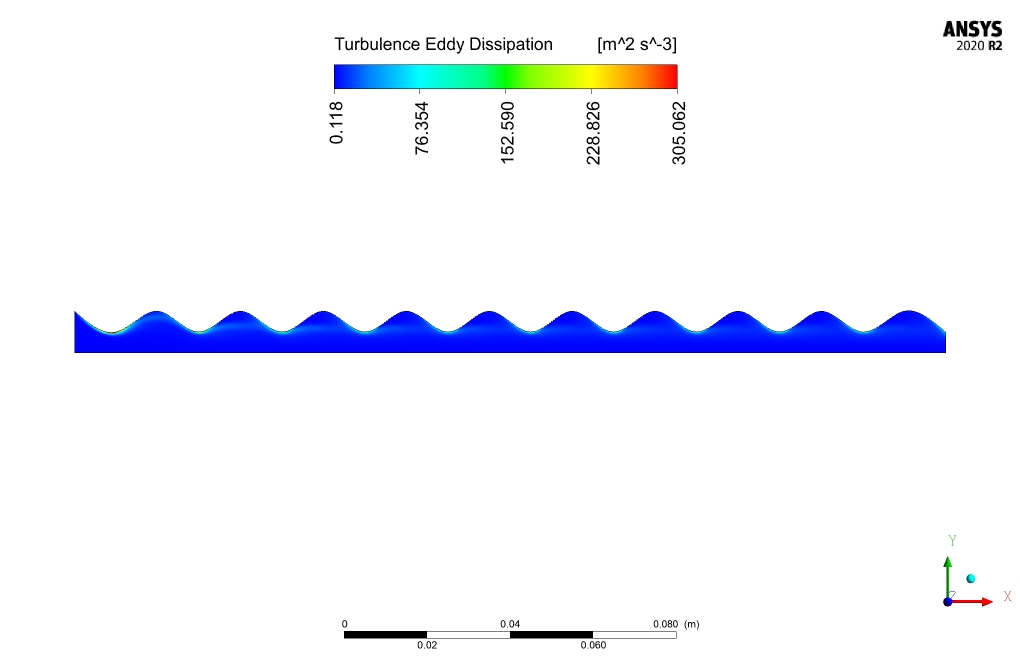
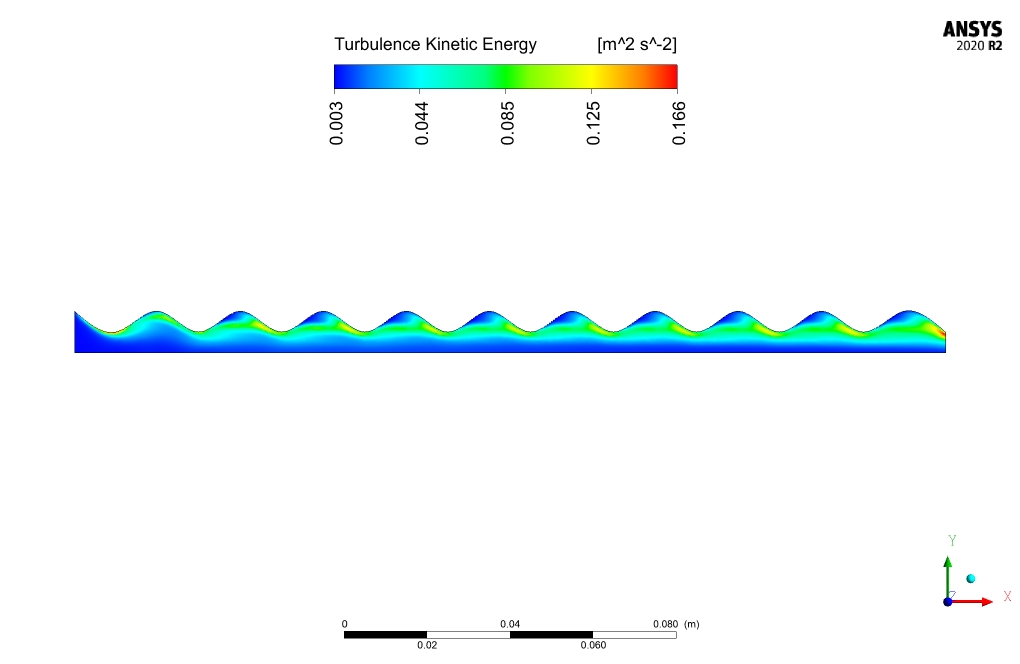
Results and discussion
The nanofluid flow average temperature at the inlet and outlet locations is 300 and 301.96K, respectively. In case of no electrical potential affecting the nanofluid, the temperature at the outlet decreases to 301.92K. Heat flux to nanofluid is equal to 72474.1 [W].
comparison between the outlet temperature of nano-fluid in the presence and absence of an electric field, reveals the effectiveness of electric field application in the present work. Electric field application increases outlet temperature by .04K and heat transfer to nano-fluid by 54W/m2.


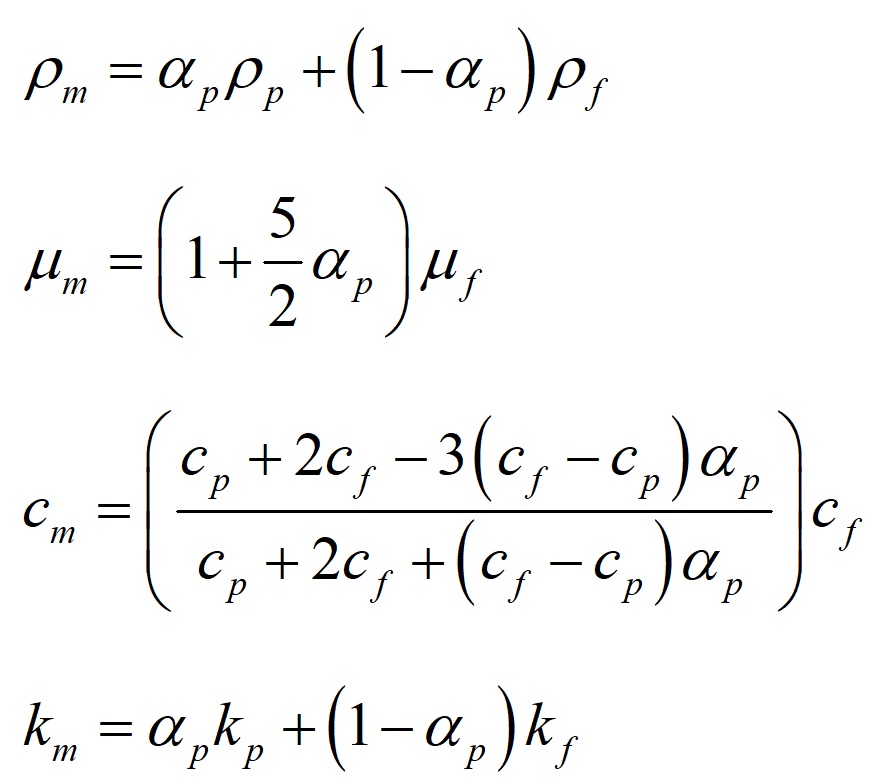



Nasir Johnston –
I see that this simulation uses the lattice Boltzmann method (LBM). Can you explain why this method was chosen over others like the finite volume method (FVM)?
MR CFD Support –
The LBM was chosen for this simulation because it is particularly well-suited for simulating complex physical phenomena such as the electric field effect on nanofluid heat transfer. It’s a mesoscopic method that bridges the gap between the macroscopic and microscopic scales, making it ideal for this type of simulation.
Cheyenne Stroman –
How does the simulation model the interaction between the nanofluid and the electric field?
MR CFD Support –
The simulation models the interaction between the nanofluid and the electric field by solving the Boltzmann equation with a force term. This force term represents the force exerted by the electric field on the charged nanoparticles in the nanofluid.
Dr. Demetrius Ortiz DVM –
Can this simulation handle different types of nanofluids and electric fields?
MR CFD Support –
Yes, this simulation can handle different types of nanofluids and electric fields. We can modify the simulation to accommodate your specific requirements.