Eulerian Two Phase Flow in a Moving Wall Cylinder, ANSYS Fluent Tutorial
$80.00 $40.00 Student Discount
- The problem numerically simulates Eulerian Two-Phase Flow in a Moving Wall Cylinder using ANSYS Fluent software.
- We design the 3-D model by the Design Modeler software.
- We Mesh the model by ANSYS Meshing software, and the element number equals 11880.
- We use the Eulerian multiphase model to define two-phase flow including water and air.
- We apply rotational velocity for the inner wall as Moving Wall.
To Order Your Project or benefit from a CFD consultation, contact our experts via email (info@mr-cfd.com), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via info@mr-cfd.com after you buy the product.
Description
Description
The present problem simulates Eulerian Two-Phase Flow in a Moving Wall Cylinder by ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.
The system consists of two different fluids, including water as the primary and secondary fluids (with a density of 2610 kg.m-3 and a viscosity of 0.0026 kg.m-1.s-1).
The two-phase flow enters the chamber in the form of a hollow cylinder. The water fluid enters the cylindrical system with a velocity of 0.629 m/s and a volume fraction of 0.67, the secondary fluid with a velocity of 0.099 m/s and a volumetric fraction of 0.23, and under relative pressure conditions of 1379000 pascals.
We design the 3-D geometry of the present model using Design Modeler software. The geometry consists of two outer and inner cylinders, through which the two-phase fluid flows through the space between the outer and inner walls. The input and output of the model are in the form of hollow circles.
We mesh the present model using ANSYS Meshing software. The mesh type is unstructured, and the element number is 11,880.
Eulerian Methodology
Therefore, we use the Eulerian multiphase model to define the flow of two fluids in the system. The outer wall of the cylinder is stationary, while the inner wall is a moving wall with a rotational speed around the central axis of the cylinder of 30 rpm.
The present model considers the standard k-omega turbulence model with shear flow correction capability and the dispersed turbulence model for multiphase flow.
Eulerian Conclusion
This project investigates the rotating wall’s effect on Eulerian multiphase turbulent flow.
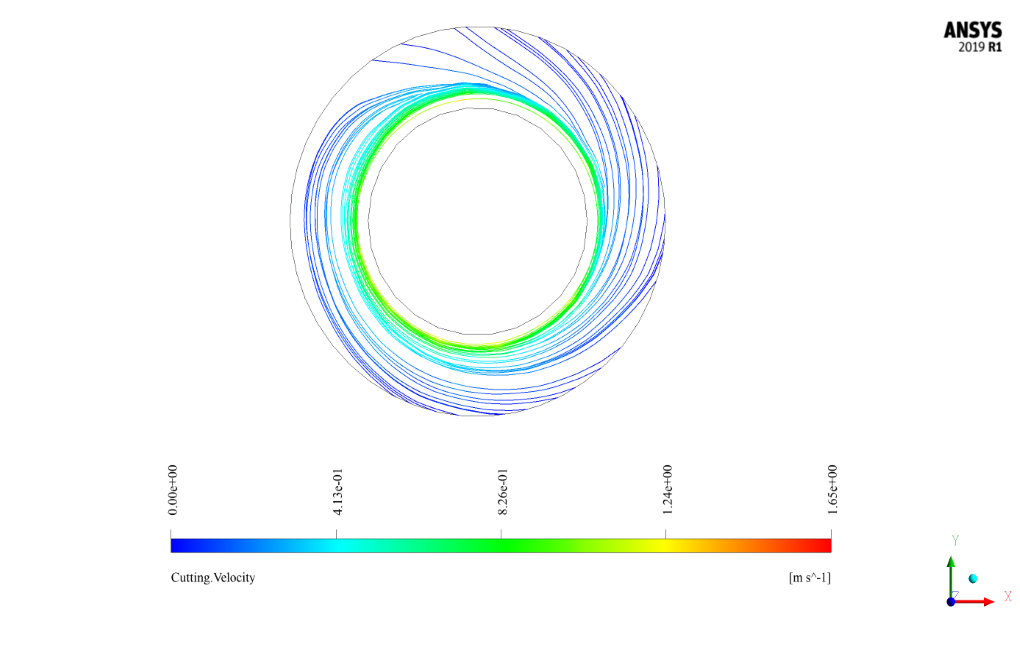
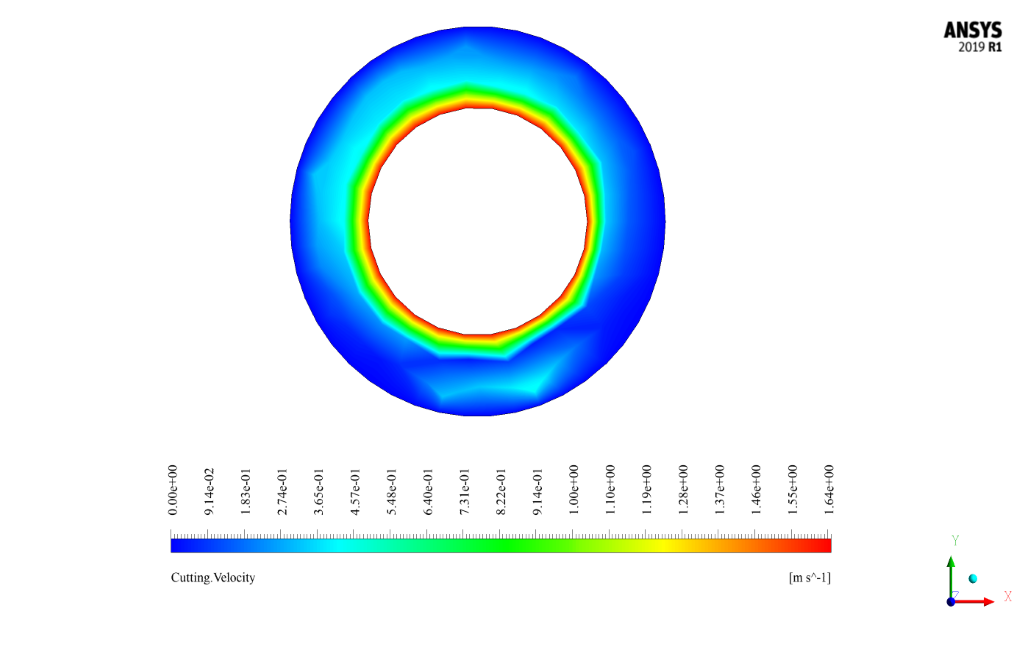
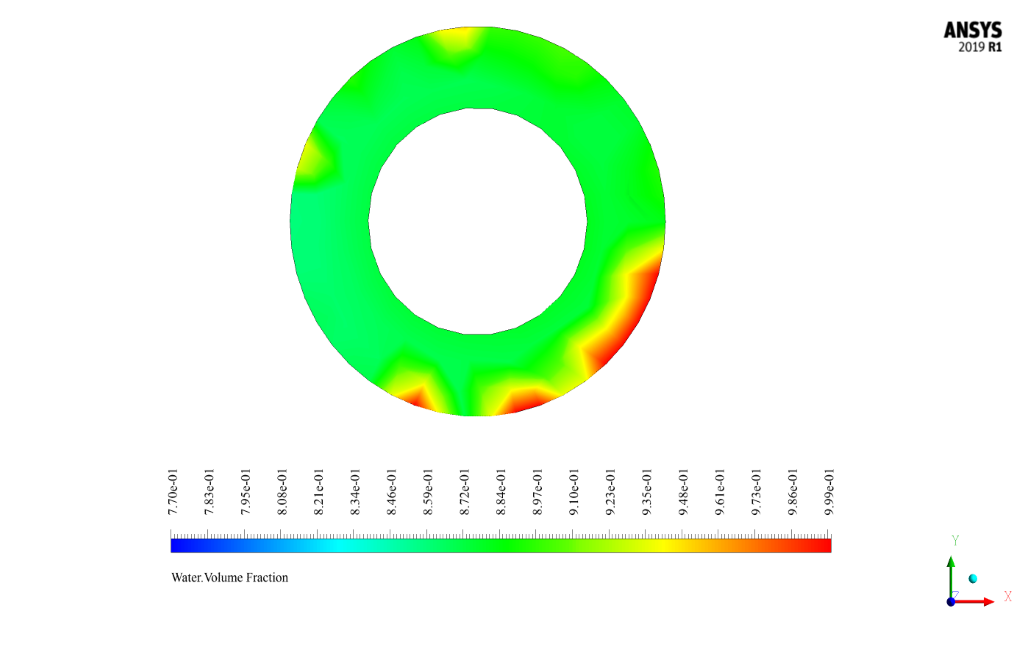
After the solution process, the two-dimensional and three-dimensional contours related to pressure (for mixing), velocity (for water phase and secondary fluid phase), the volume fraction of water and secondary fluid, as well as path lines (water and secondary fluid), have been obtained.
Two-dimensional contours are presented in two sections, YZ and XY. The YZ section is defined as passing through the central axis of the cylinder, and the XY section is perpendicular to the cylinder’s central axis at intervals of 4, 9, and 13.716 (output) meters from the input section.

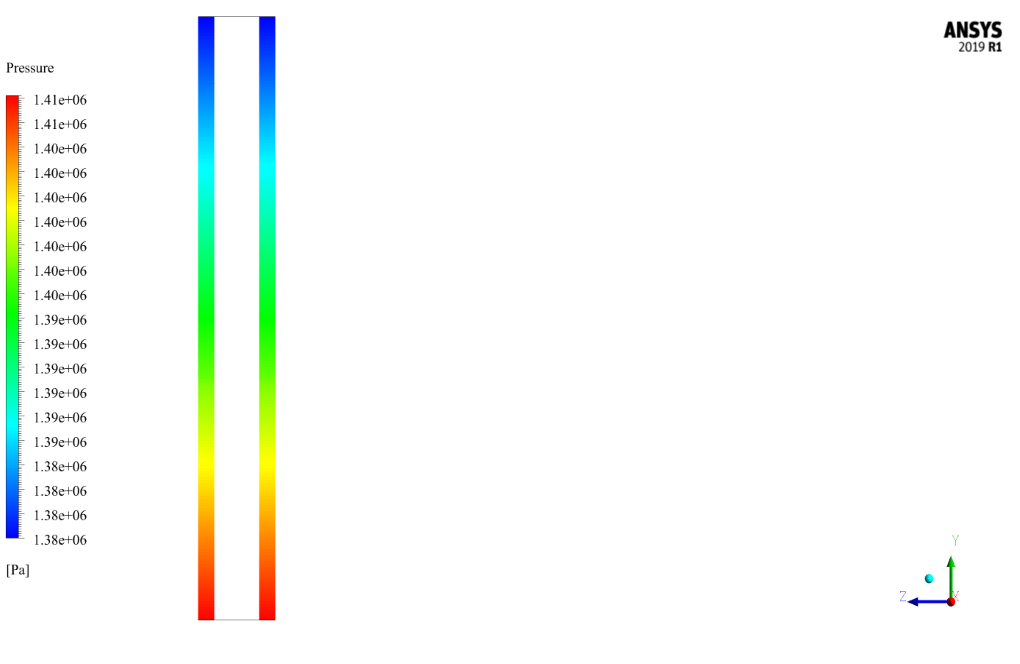
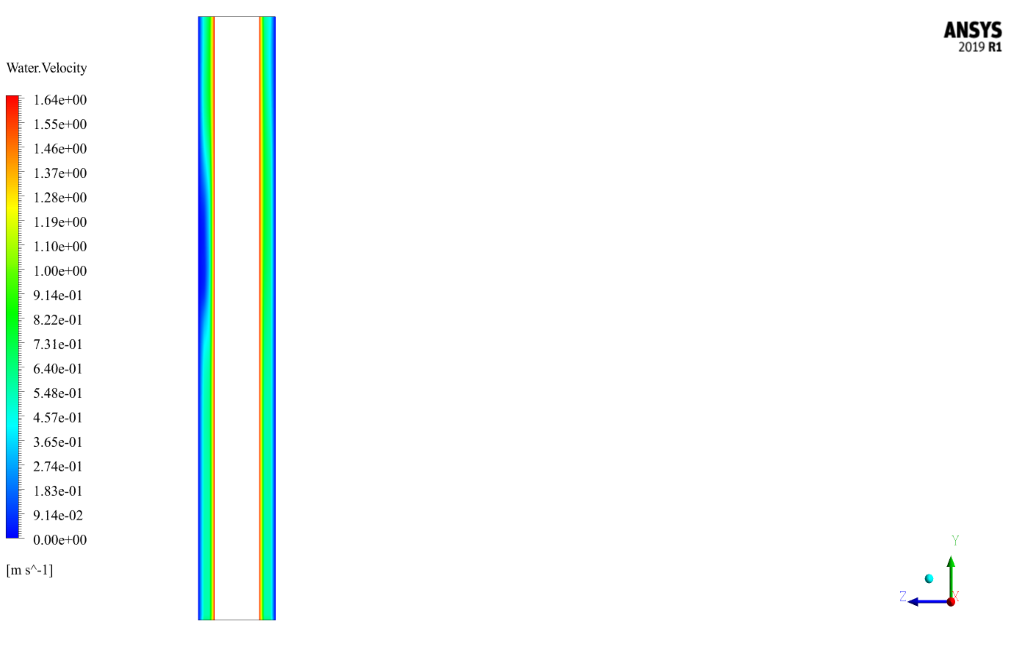







Jeanie Gerhold –
How are the results of the simulation visualized?
MR CFD Support –
The results are visualized using contour plots of pressure, velocity, and volume fraction of the phases. The movement of the wall is visualized using a dynamic mesh animation.
Ms. Clare Lind –
well done! keep it up.
Jevon Abernathy –
I am utterly fascinated with the visualization in the tutorial! The contours are so detailed and provide excellent clarity on the multiphase flow patterns. Well done on capturing the complexities!
MR CFD Support –
Thank you for your kind words! We’re delighted to hear that you found the visualizations detailed and helpful. It’s our aim to provide clear and insightful resources to enhance the understanding of such complex simulations. We appreciate your feedback!
Adaline Kris PhD –
The tutorial seems comprehensive, but I’m curious, how is the discrepancy in fluid velocities between the primary water fluid and the secondary fluid managed within the CFD model? Does this difference in velocity cause any particular challenges during simulation?
MR CFD Support –
In the given Eulerian multiphase CFD model, the discrepancy in fluid velocities is managed using the Eulerian multiphase approach. This approach allows the simulation of multiple interacting fluid phases with differing velocities and properties. The governing equations for each phase are solved individually and are coupled through pressure and interphase exchange coefficients. The challenge of different velocities can lead to complexities in terms of stability and convergence requiring carefully chosen mesh sizes, time steps, and numerical schemes. However, these challenges are accounted for when setting up the simulation parameters to ensure that the model realistically captures the behavior of both phases.
Allan Abernathy –
The tutorial sounds comprehensive. Seeing the effects of rotation in a multiphase flow system must be fascinating! The velocity and volume fraction contours would be particularly interesting to study.
MR CFD Support –
Thank you for your kind words! We are thrilled to hear that you found the tutorial on Eulerian Two-Phase Flow in a Moving Wall Cylinder informative and fascinating. It’s always exciting to see the dynamic interactions within a multiphase system, especially with the added complexity of rotational effects on flow dynamics. Should you have any more feedback or require further learning materials, feel free to let us know!
Mrs. Hassie Konopelski –
What exactly does the shear flow correction capability add to the simulation, and in what scenarios would it be most beneficial?
MR CFD Support –
The shear flow correction in the standard k-omega turbulence model allows for more accurate predictions of the turbulence characteristics in shear flows, which are common in industrial mixing applications. It corrects for the effect of shear strain on turbulence kinetic energy, which improves the model’s performance in predicting the flow, especially in the near-wall regions. It is most beneficial in scenarios involving complex turbulence interactions such as swirling and rotating flows, like the flow inside a cylinder with a rotating wall in this case.
Frederik Lebsack –
Can you clarify how the interaction between the moving inner wall and the fluids were handled computationally in the simulation?
MR CFD Support –
In this simulation, the interaction between the moving inner wall and the fluids is computed using the moving mesh technology. The inner wall’s rotational movement was set to 30 RPM, and this dynamic boundary condition altered the flow behavior of the two fluids within the gap between the inner and outer walls, which was continually recalculated as part of the simulation. This approach allowed for accurate simulation of the effects this moving boundary had on the flow characteristics, including the local shear rates and the fluid velocities.
Houston Reilly V –
Can this simulation be used to optimize the design of the cylinder or the movement of the wall?
MR CFD Support –
Absolutely! The results from this simulation can provide valuable insights into the behavior of the two-phase flow and the effect of the moving wall, which can be used for design optimization.
Bettye Kling –
The simulated results are absolutely insightful! The clear two-dimensional contours enhanced my understanding of the phase distribution. How does the cylinder’s rotation speed affect the mixing efficiency of the two fluids?
MR CFD Support –
Hello! I’m glad to hear you found the simulation helpful. The cylinder’s rotation speed induces a tangential force on the fluids, promoting mixing by generating secondary flow structures like vortices. As the rotation speed increases, the mixing efficiency typically improves up to a certain point, after which it might cause excessive turbulence that could potentially lead to a less stable phase interface.
Tina Boyer –
The tutorial was insightful! After watching, it seems that Eulerian modeling can tackle some complex flow scenarios. The level of details in setup and explanation made me understand the interaction between two fluid phases quite a lot!
MR CFD Support –
Thank you for your positive feedback! We are thrilled to hear that our tutorial on Eulerian Two-Phase Flow in a Moving Wall Cylinder has enhanced your understanding of fluid interactions in complex scenarios. Your appreciation means a lot, and it motivates us to keep producing high-quality educational materials. If you ever have more questions or require further assistance, please feel free to reach out!
Holly Price –
I need some clarification on how the rotational movement of the inner wall affects the multiphase flow. Can you elaborate on that with the results derived from the study?
MR CFD Support –
Certainly! The rotational movement of the inner wall introduces a centrifugal force to the fluids inside the cylinder. As a consequence, this influences the flow pattern and induces a radial pressure gradient that can lead to secondary flow structures across the flow field. Specifically, the results show that the rotational movement impacts the mixing behavior of the two phases leading to an increase in the radial velocity components. Simultaneously, it affects the distribution of the volume fractions for both fluids along the radial direction of the cylinder. The contours of velocity and volume fraction display these effects, revealing the complexities that arise when a rotating wall interacts with Eulerian two-phase flow.
Adele Armstrong –
The tutorial sounds very comprehensive, but I’m curious, what challenges might I face when setting up the rotational motion for the inner cylinder wall, and how can these be tackled?
MR CFD Support –
Configuring rotational motion for the inner cylinder wall can be achieved by specifying the wall motion conditions in ANSYS Fluent to rotate at the specified rotational speed. The motion can be defined as a moving wall boundary condition relating rotational speed and/or velocity to the wall. To ensure accurate setup, it is crucial to define the axis of rotation correctly in relation to the cylinder geometry. If you face challenges like the setup not behaving as expected, you might need to double-check that the axis of rotation is accurately defined, that the mesh quality around the moving parts is sufficient to capture the dynamics, and that the time step is small enough to resolve the rotations accurately. The tutorials provided by MR CFD Company will guide you through handling these setup procedures.
Adaline Mitchell –
I always had trouble with understanding the Eulerian multiphase model, but this tutorial explained everything so clearly! The visuals of pressure and velocity changes in different sections made it much more comprehensible.
MR CFD Support –
Thank you for your positive feedback! We’re thrilled to hear that our tutorial on the Eulerian multiphase model in a moving wall cylinder was helpful to you and that the visuals aided your understanding. If you have any more questions or need further assistance with ANSYS Fluent, please don’t hesitate to reach out.
Amalia Doyle MD –
I was really impressed by the detail on the multi-phase flow dynamics in your simulation, particularly how the moving wall influenced the flow. Was adjusting rotational velocity an element that could be studied for optimization in this simulation?
MR CFD Support –
Thank you for your kind words! Yes, in the simulation, you can definitely explore how varying the rotational speed of the moving wall impacts the flow properties and potentially optimize it for different outcomes.
Deshawn Wiegand –
I’m fascinated by the physics behind the Eulerian multiphase flow in this tutorial. Can you explain how the different rotation speeds of the inner and outer walls affect the flow dynamics inside the cylinder?
MR CFD Support –
In this simulation, the inner wall of the cylinder is moving with a rotational speed of 30 rpm, while the outer wall is stationary. The different speeds create a shear effect and induce a rotational flow pattern, known as Taylor-Couette flow, between the walls. This flow pattern greatly influences the mixture homogeneity, velocity distribution, and turbulence within the two fluids. The moving wall injects momentum into the system, affecting the primary and secondary fluid flow behaviors differently due to their disparate physical properties.