Frictional Force of a Fluid Flow Mixed With Particles
$140.00 $70.00 Student Discount
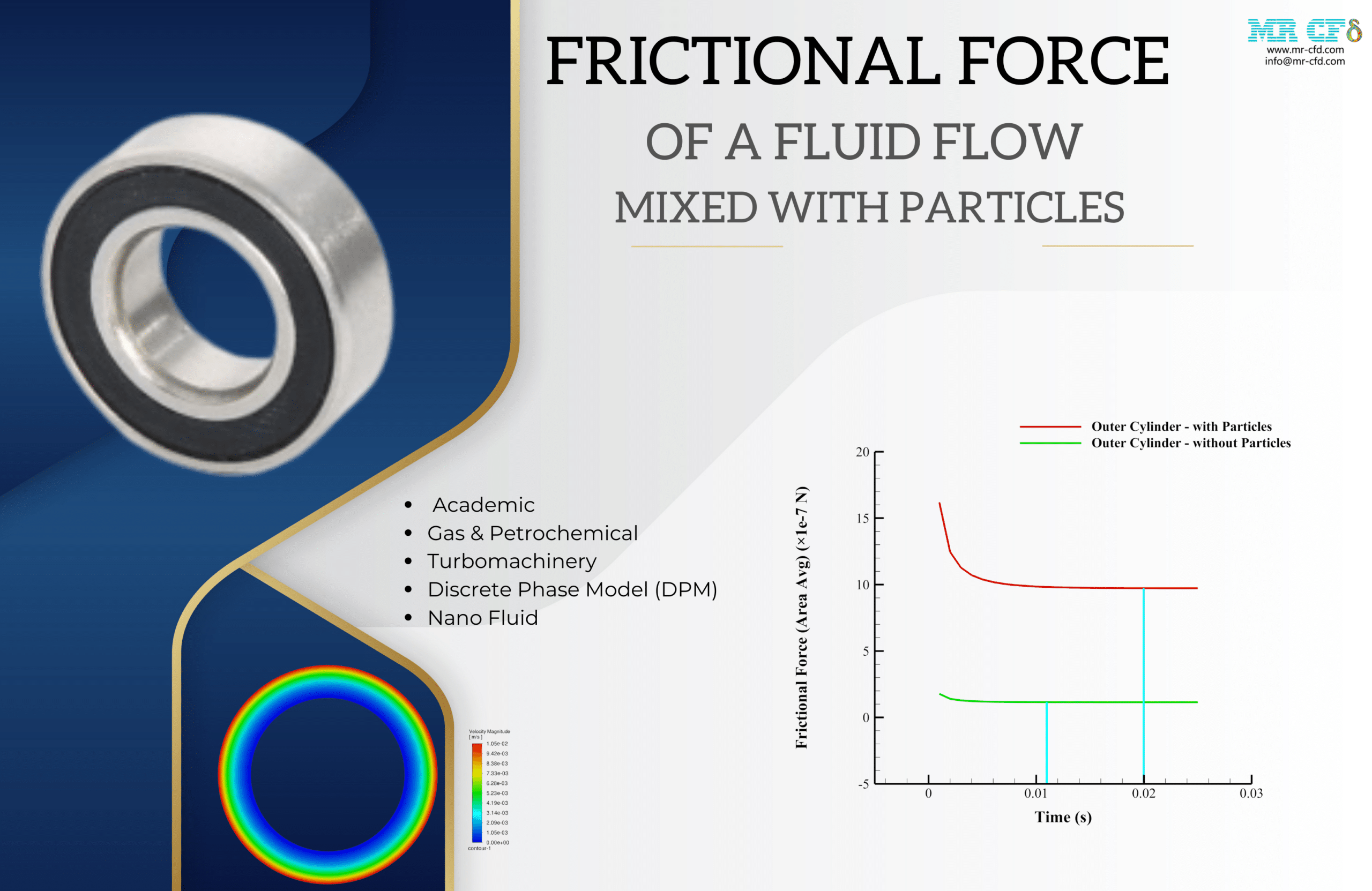
- This report presents a simulation examining how particle presence affects the friction force on the walls of two concentric cylinders using the Discrete Phase Method (DPM).
- The geometry of the two concentric cylinders was created using ANSYS SpaceClaim software.
- A high-quality mesh of 51840 hexahedral elements was generated using ANSYS Meshing software.
- Appropriate DPM settings were applied and the friction force exerted on the two cylinder walls was calculated.
To Order Your Project or benefit from a CFD consultation, contact our experts via email (info@mr-cfd.com), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via info@mr-cfd.com after you buy the product.
Description
Frictional Force Exerted on the Wall of Two Concentric Rotating Cylinders: Investigation of The Effect of Particle Presence, ANSYS Fluent Training
Description
In some industries such as Microelectromechanical Systems and microfiltration systems, micro-channels or micro-bearings with micrometer-scale flow thickness can carry particles of nanometer-scale. In these conditions, the effect of particles being carried on the frictional force applied on the wall of these microchannels and micro-bearings will be very important. In this study, ANSYS Fluent is employed to simulate the Discrete Phase Model (DPM) problem, focusing on investigating the difference in frictional force on the micro-bearing wall with and without the presence of particles. The particles used are spherical anthracite particles with a diameter of 400 nanometer. Also, the interaction between particles and fluid is considered.
The investigated geometry consisted of two concentric cylinders with diameters of 100 and 70 micrometers, which were drawn by ANSYS SpaceClaim software. The outer cylinder is rotating and the inner cylinder is stationary. ANSYS Meshing was employed to generate a high-quality mesh comprising 51,840 hexahedral elements. This mesh density provides sufficient resolution to accurately capture the flow dynamics, turbulence effects, and particle distribution within the domain. The mesh element size is larger than the particle size to ensure proper particle tracking.
Methodology
A pressure-based, transient solver was employed to monitor the particle injection in time and capture the interaction between the particles and the fluid. Polyalphaolefin (PAO) 68 was used as a fluid between the two cylinders. The SST k-omega turbulence model was adopted for this simulation due to its effectiveness in capturing the complex flow characteristics that arise in the rotational cylinder. A suitable wall function was implemented to accurately resolve the near-wall region, which is essential for capturing detailed interactions between fluid flow and particle dynamics near the cylinder walls, as well as the resulting frictional force. Additionally, appropriate forces and models related to particle dynamics were considered to enhance the accuracy of the Discrete Phase Model (DPM) settings used in the analysis.
Results and Conclusion
From the simulation, the following results are obtained:
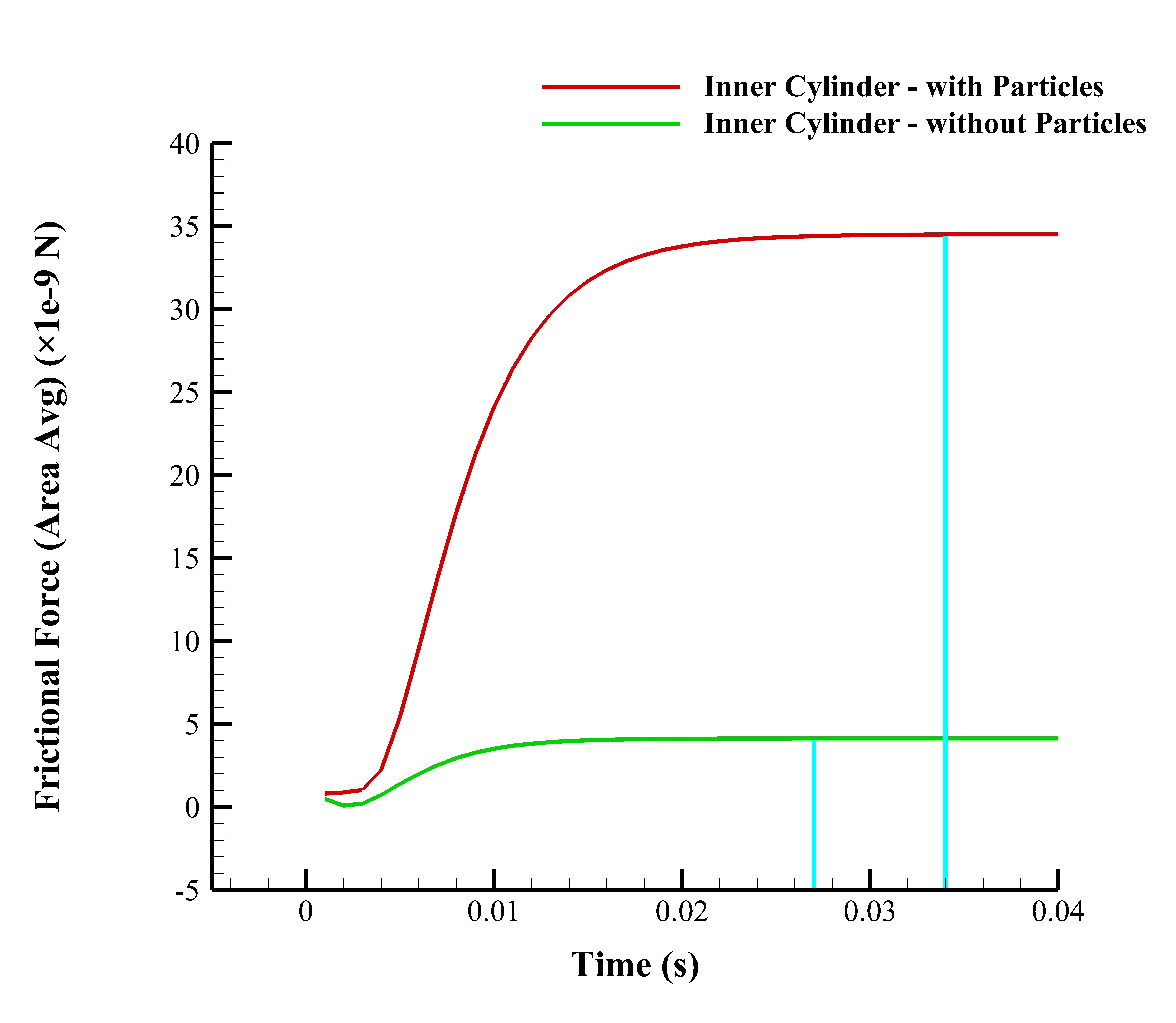
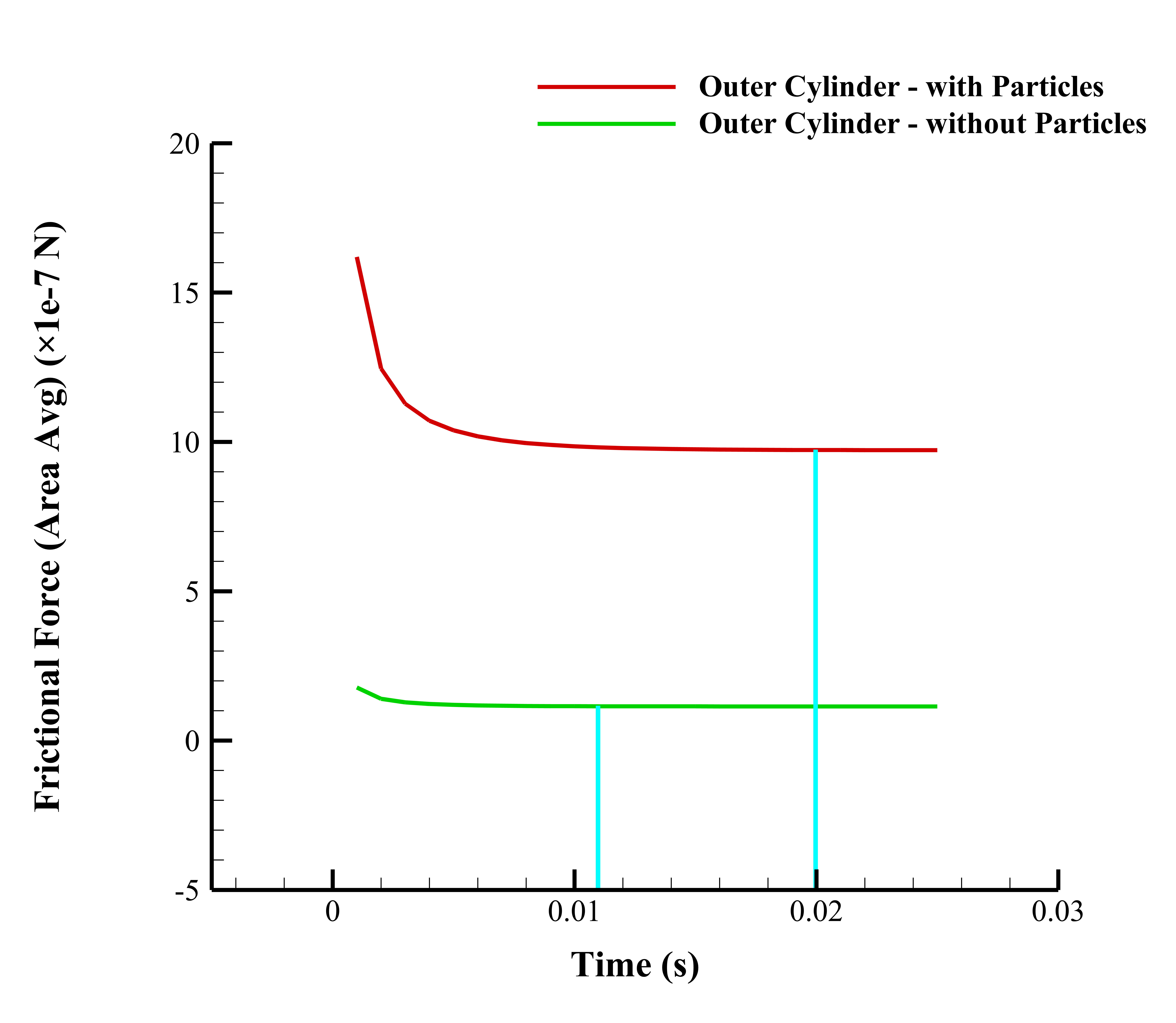
- The frictional force on the inner wall of the cylinder increases with time, while on the outer cylinder, the frictional force on the wall decreases with time.
- The frictional force on the outer cylinder’s wall in both with and without particles, is greater than the frictional force on the inner cylinder’s wall. This might be because the outer cylinder is rotating and the frictional force is proportional to the velocity gradient.
- The frictional force on the cylinder wall is increased in the scenario where particles are present. This is because these particles can enhance the effective viscosity of the medium which leads to an increase in frictional force.
- As it is clear from the plots, for the inner cylinder and without the presence of particles, the problem reached a steady state after 27 milliseconds, and with the presence of particles, the problem became steady after 34 milliseconds. Also, for the outer cylinder without the presence of particles, after 11 milliseconds and with the presence of particles, after 20 milliseconds, the problem has become steady state. Therefore, in general, it can be concluded that for the condition of without the presence of particles, the problem has reached a steady state after 27 milliseconds and for the condition of with the presence of particles, the problem has reached a steady state after 34 milliseconds.


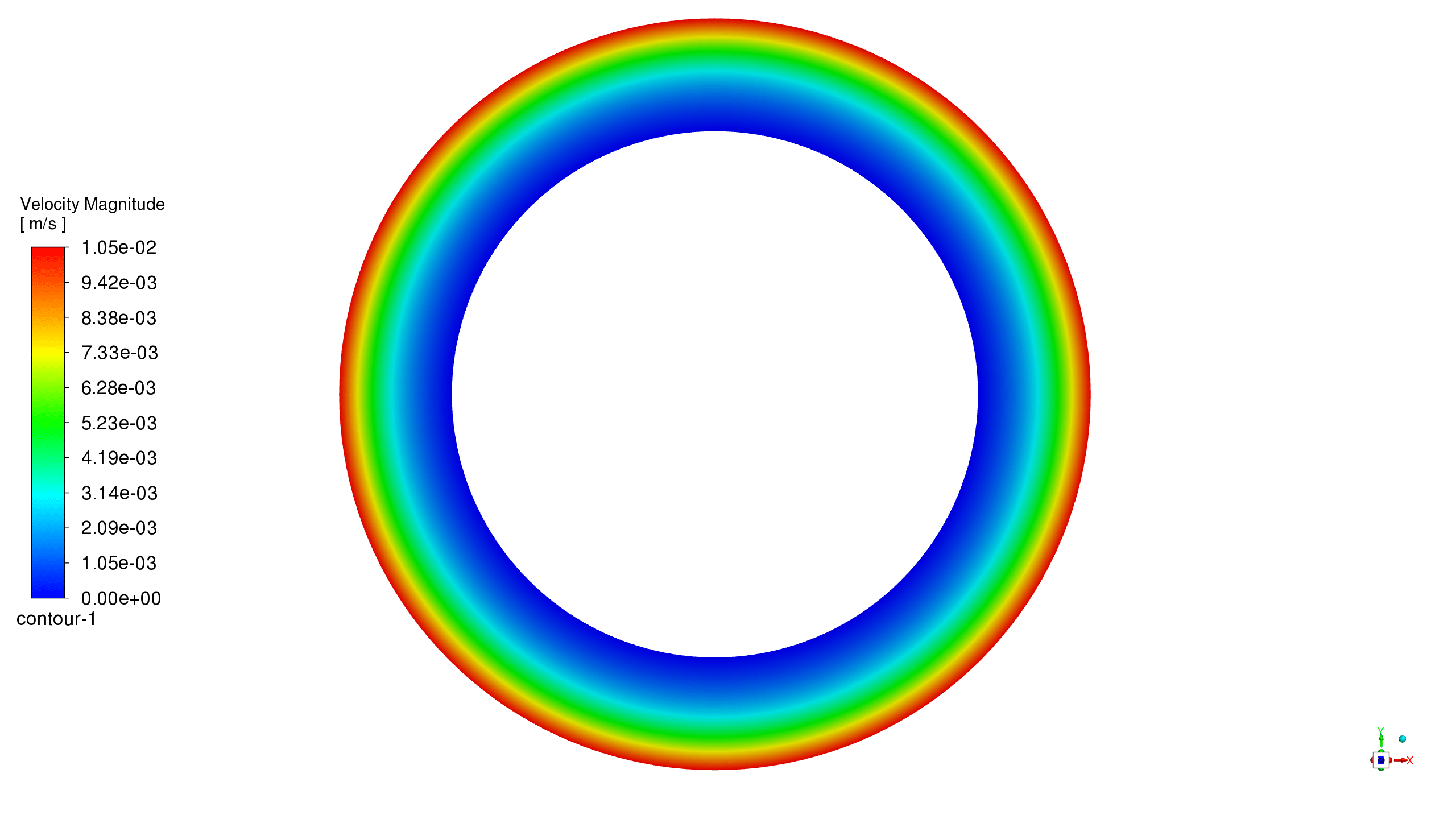





Reviews
There are no reviews yet.