Optimization of Wing Lift-to-Drag Ratio for the Northrop Grumman RQ-4 Global Hawk with RBF Morph
$150.00 $75.00 Student Discount
- The problem numerically simulates the Northrop Grumman RQ-4 Global Hawk using ANSYS Fluent
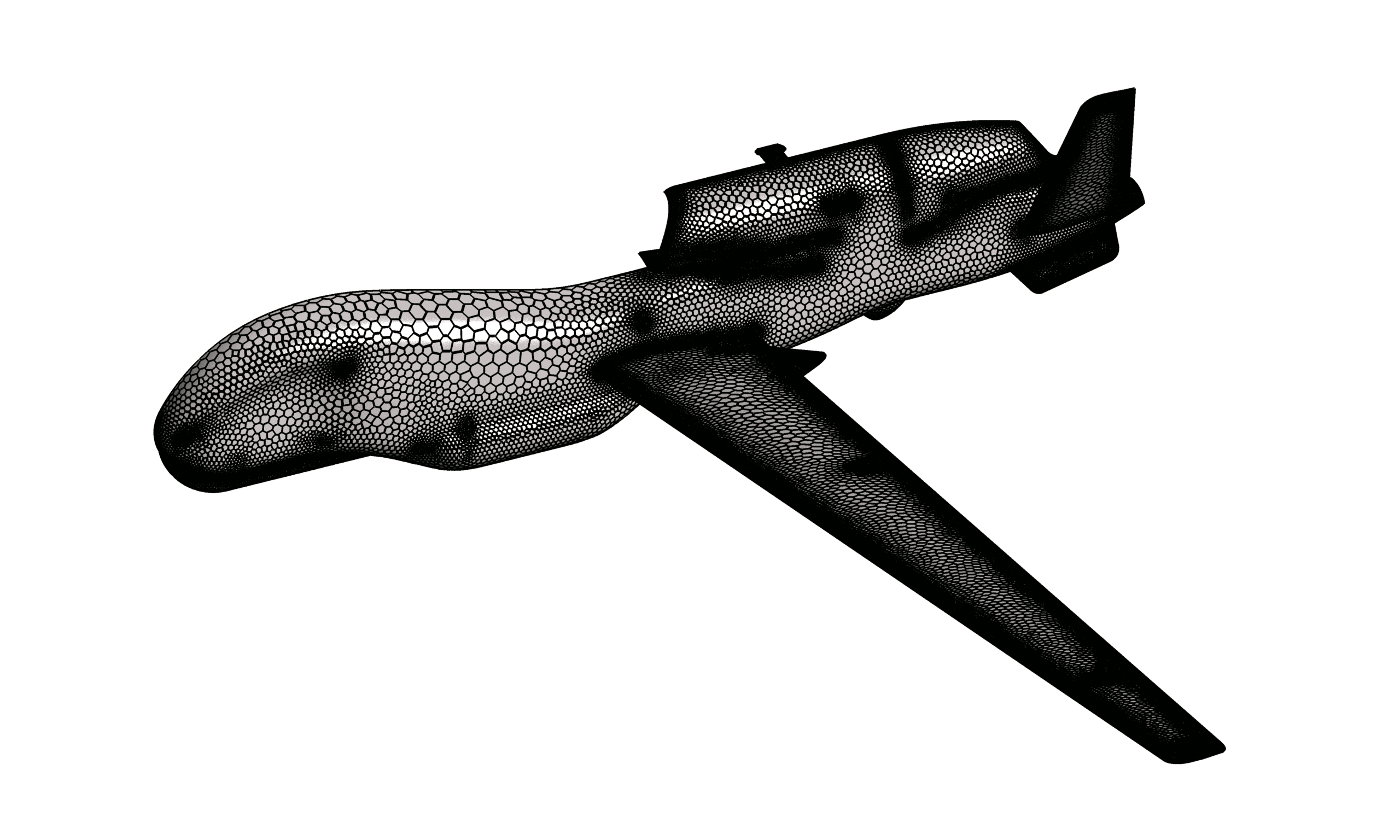
- The geometry is designed in SpaceClaim, and the meshing is performed using fluent Meshing.
- The mesh type is polyhedral, and the element number equals 2,063,629.
- We aim to Maximize the Lift-to-Drag Ratio of wings.
- We use the Adjoint Solver to analyze the Shape Sensitivity.
- The Design Optimization is performed with the Gradient-based
- The Radial Basis Function (RBF) is used to apply Mesh Morphing.
To Order Your Project or benefit from a CFD consultation, contact our experts via email (info@mr-cfd.com), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via info@mr-cfd.com after you buy the product.
Description
Optimization of Wing Lift-to-Drag Ratio for the Northrop Grumman RQ-4 Global Hawk with RBF Morph Using ANSYS Fluent
Description
This project is related to the aerodynamic simulation of the Northrop Grumman RQ-4 Global Hawk using Ansys Fluent software. We aim to optimize the Design of this model using an Adjoint Solver and Gradient-Based Optimizer. Such modeling is done in Three stages. First, we perform the aerodynamic simulation. In the second step, we analyze the Sensitivity with the adjoint solver. Finally, we change the model’s design to achieve Optimal performance with the gradient-based optimizer.
The adjoint solver provides a series of data that is expressed in the form of sensitivity analysis. We focus on Shape sensitivity. This tool identifies which areas of the geometry have the greatest influence on system performance. So we need to define a target parameter. This output parameter is called Observable. In the present work, we have defined the Lift-to-Drag Ratio as observable.
Therefore, the adjoint solver is based on the Lift-to-Drag Ratio in wings. Wherever more sensitivity is shown, i.e., Displacement of the boundary or Deformation of the shape of the design, it has a greater effect on the Lift-to-Drag Ratio. We use the sensitivity analysis data in the gradient-based optimizer. In this tool, we specify how the observable should be changed. For example, in this project, we consider increasing the Lift-to-Drag Ratio. These changes should lead to an optimal design.
We modeled the geometry of the project using SpaceClaim software. Then we meshed the model with Fluent Meshing software. The model mesh is un-structured polyhedral, and the number of cells is equal to 2,063,629.
You can view the aerodynamic and FSI simulation of this product from here.
Adjoint Solver Methodology
To apply mesh changes, we used the Mesh Morphing technique. There are three methods for mesh morphing: polynomial, direct interpolation, and Radial Basis Functions (RBF). In this project, we used RBF for mesh morphing. For the radial basis function, the mesh deformation is interpolated from the control points. In the Objective part, we determined the value of observable changes target by 5 %.
Adjoint Solver Conclusion
The present simulation is done in three consecutive steps. So we investigated the results in three steps. In aerodynamic simulation, we obtained velocity and pressure contours. These contours showed the distribution of velocity and pressure inside the domain. We analyzed the sensitivity in the adjoint solution. We obtained the shape sensitivity contour on the wings. The highest sensitivity means that boundary displacement and shape deformation in these areas have the greatest effect on the value Lift-to-Drag Ratio.
Results
In the final solution by the gradient-based optimizer, the geometry undergoes deformation. The Lift-to-Drag Ratio before optimization was equal to 7.96526. After performing the second and third steps, this Lift-to-Drag Ratio reached the value of 8.09169. So we conclude that the Lift-to-Drag Ratio has increased by 1.15 %. We can see the shape deformation and boundary displacement. The maximum boundary displacement is equal to 3.2415e-4 m, and the average displacement is equal to 5.1548e-5 m.
Optimized Wing Geometry As observed in the contour plot of the z-component of the wings post-optimization, the winglet exhibits a slight increase in size. This geometric modification is consistent with enhancing lift generation. The enlarged winglet effectively reduces wingtip vortices, thereby improving the overall aerodynamic efficiency of the RQ-4 Global Hawk’s wing structure.
Pressure Distribution Analysis of the pressure gradient in the vicinity of the winglet, both upstream and downstream, reveals a notable reduction post-optimization. This decrease in pressure differential is indicative of a reduction in drag forces acting on the wing. The optimized winglet geometry contributes to a more favorable pressure distribution, which is crucial for minimizing induced drag and improving the overall lift-to-drag ratio. velocity contours for pre- and post-optimization configurations are presented.
In summary, the computational optimization process utilizing ANSYS Fluent has yielded promising results in terms of improving the lift-to-drag ratio of the Northrop Grumman RQ-4 Global Hawk’s wing.




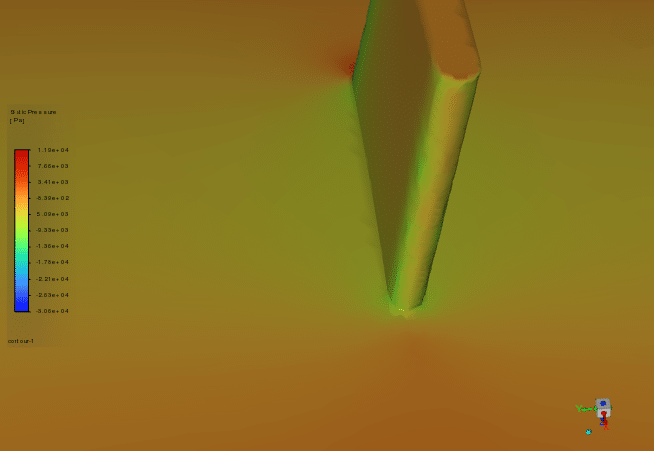







Reviews
There are no reviews yet.