Quadcopter Dynamic Stability Derivatives, Ansys Fluent CFD Simulation

Description

This project aims to obtain dynamic stability derivatives for a Quadcopter, a type of helicopter or multicopter with four rotors.

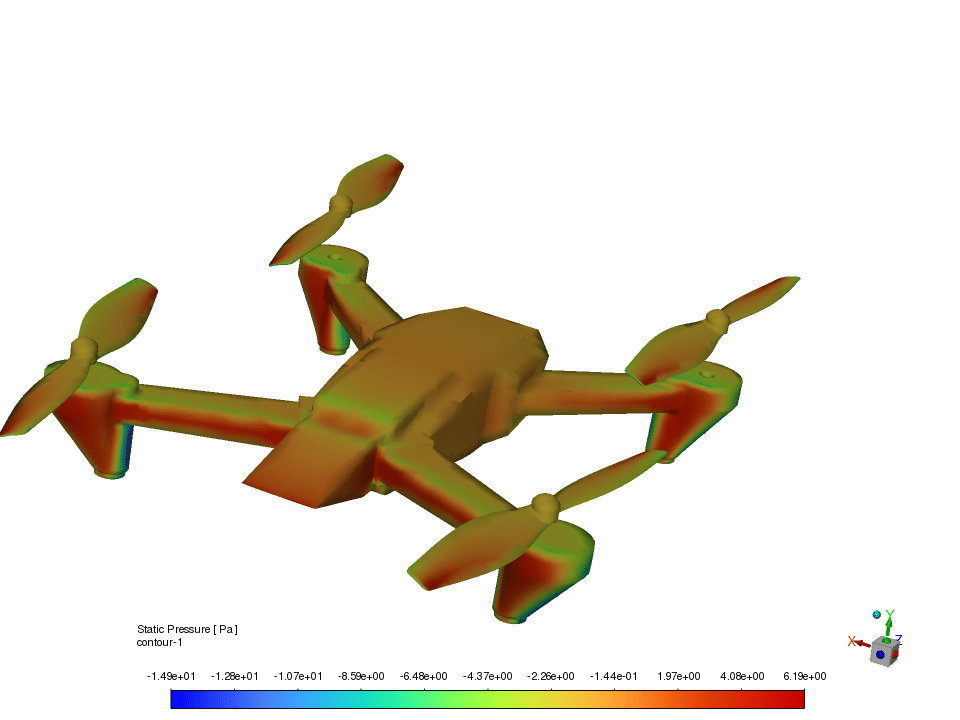
The geometry of the Quadcopter is meticulously designed using SpaceClaim software, ensuring high fidelity to the actual Quadcopter.

An unstructured mesh grid is generated using ANSYS Meshing software to discretize the computational domain. The resulting mesh comprises 1,710,236 cells, providing a detailed representation of the flow field around the Quadcopter.

you can Also visit Quadcopter Acoustic and FSI Simulation.

Methodology

we employ ANSYS Fluent software and leverage the applications of Computational Fluid Dynamics (CFD) in flight dynamics to obtain the necessary derivatives. In this simulation, we developed a User-Defined Function (UDF) file to accurately model the Quadcopter’s motion during flight.

To simulate the Quadcopter motion, we employ mesh motion techniques and UDF files. The simulation is set up with a velocity of 5 m/s and an operating pressure of 101,325 Pa, representing sea-level conditions.

The simulation begins with a Quadcopter at a zero-degree angle of attack, and a forced oscillation motion is modeled to capture the dynamic stability characteristics.

The UDF file is programmed to prescribe the desired motion of the Quadcopter, including pitch, yaw, and roll oscillations.

Also To capture the rotational motion of the quadcopter blades with an angular velocity of 600 RPM, we employed two mesh motion zones. These zones allowed for accurate simulation of the blade dynamics and airflow characteristics around the quadcopter.

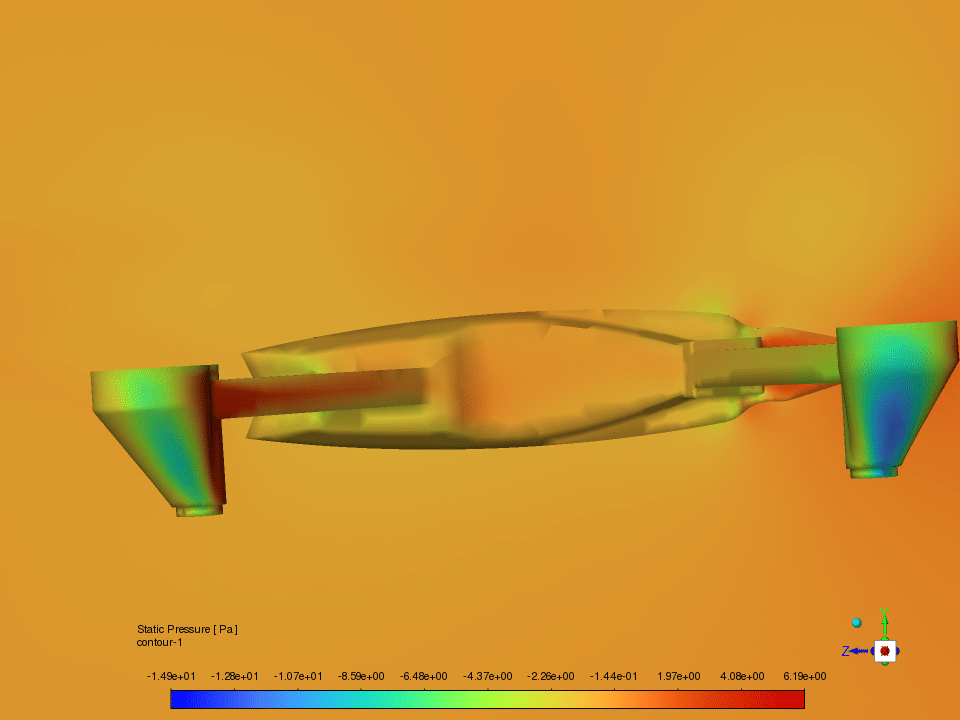
result

Post-processing the simulation results involves extracting the relevant aerodynamic coefficients, such as lift, drag, and moment coefficients, at each time step. These coefficients are then analyzed to determine the dynamic stability derivatives, including pitch damping (Cmq), yaw damping (Cnr), roll damping (C_lp), and lift force derivative (CLα).

The obtained dynamic stability derivatives provide valuable insights into the quadcopter stability and control characteristics.

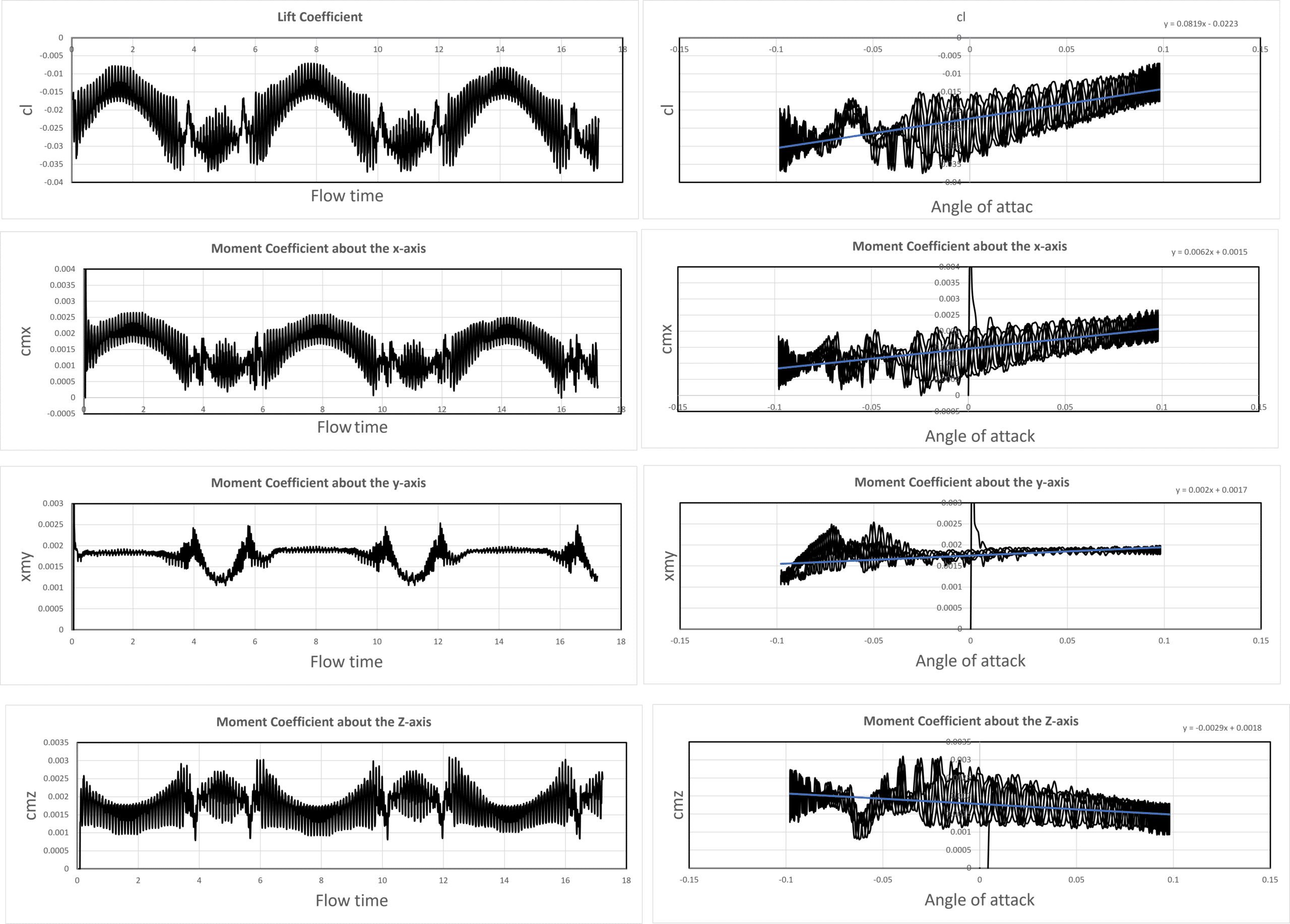
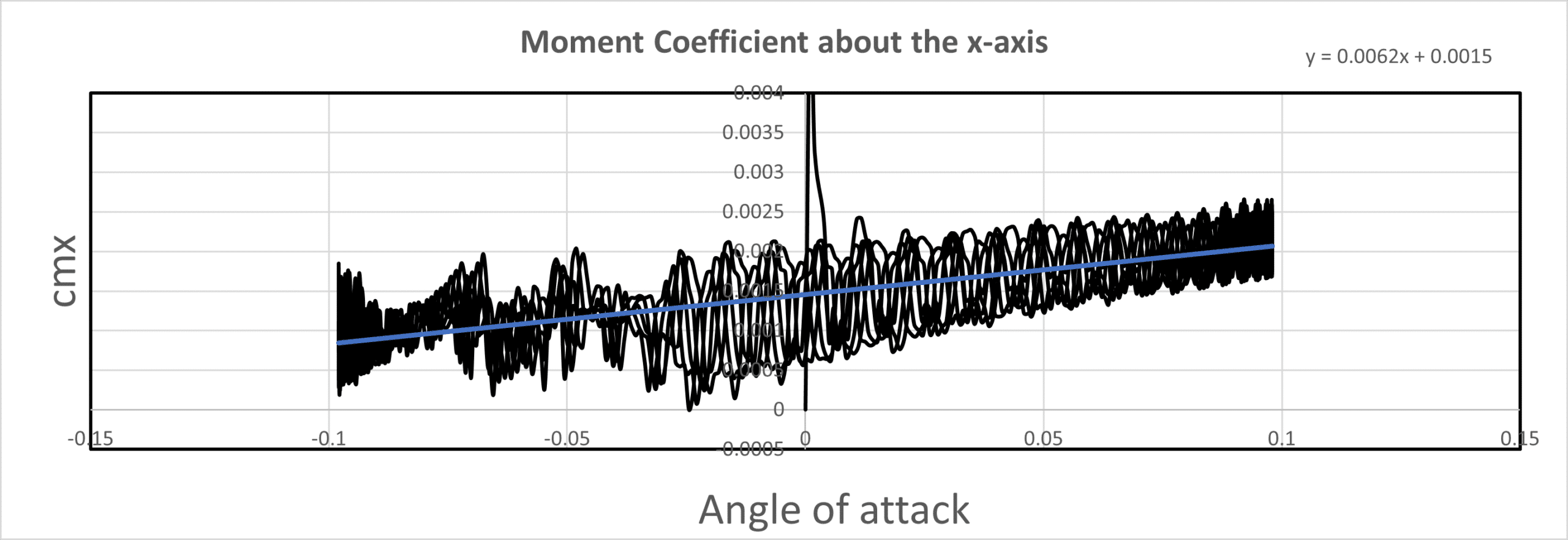
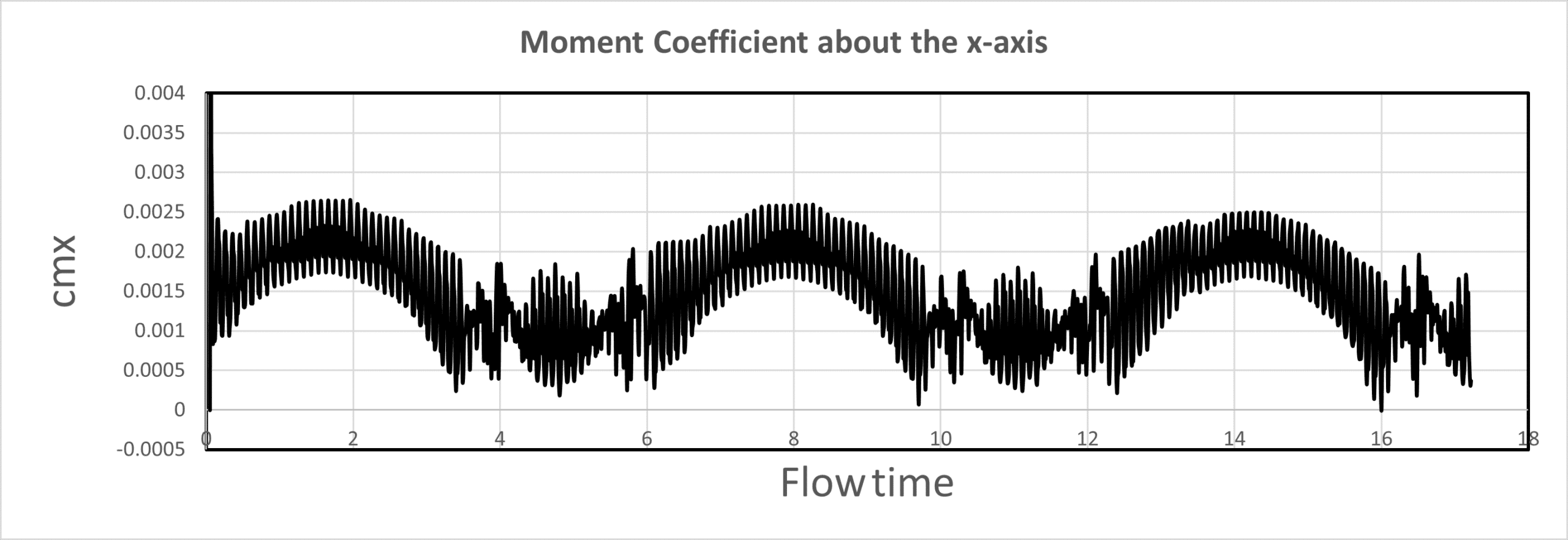
c_mx (Moment Coefficient about the X-axis):

The equation y = 0.0062x + 0.0015 indicates a positive relationship between CMx and the angle of attack. The slope of 0.0062 represents the roll moment derivative (Clp) about the x-axis, suggesting that the quadcopter experiences a piching moment as the angle of attack changes. The oscillations in CMx over the flow time and angle of attack indicate the presence of a pitch-damping moment that affects the quadcopter’s pitch stability.

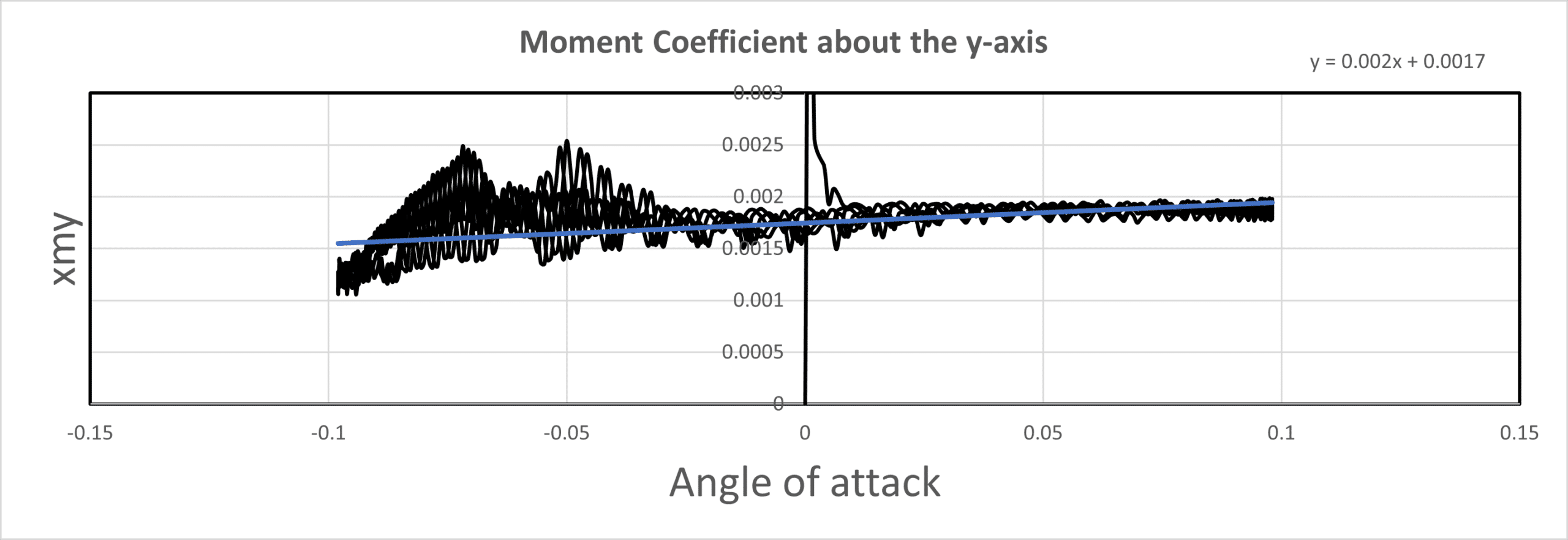
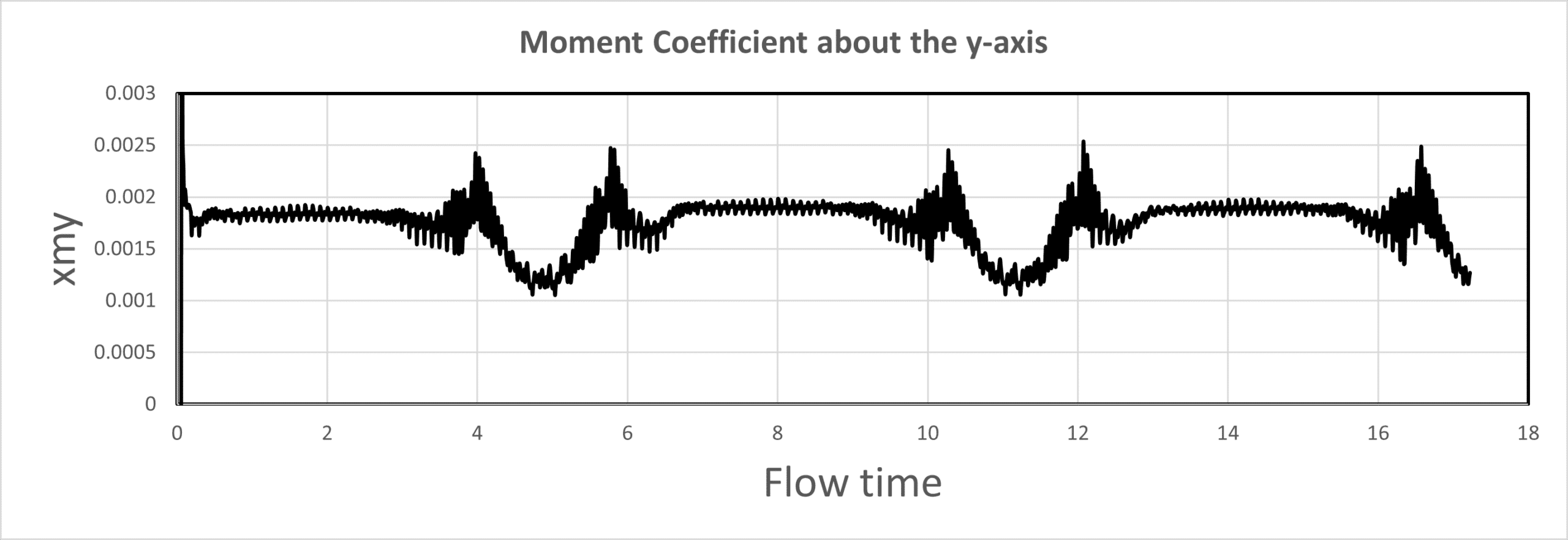
C_my (Moment Coefficient about the Y-axis):

The equation y = 0.0062x + 0.0015 indicates a positive relationship between CMx and the angle of attack. The slope of 0.0062 represents the yaw moment derivative (Clp) about the x-axis, suggesting that the quadcopter experiences a yawing moment as the angle of attack changes. The oscillations in CMx over the flow time and angle of attack indicate the presence of a roll-damping moment that affects the quadcopter’s yaw stability.

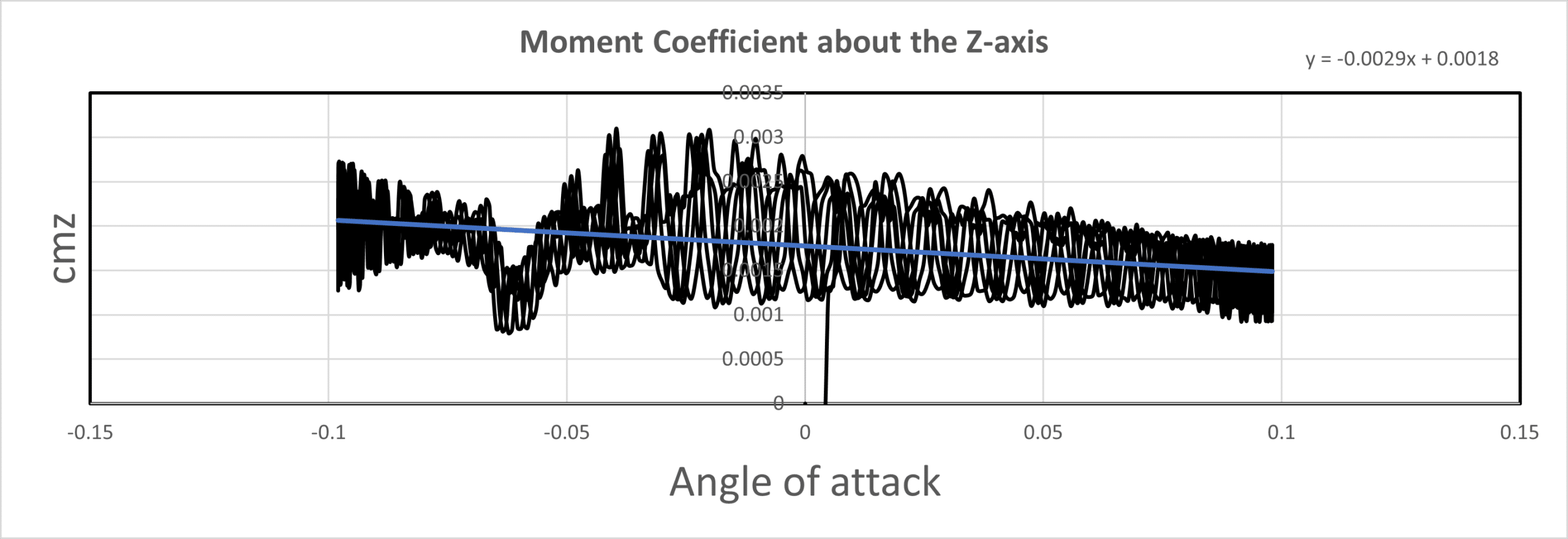
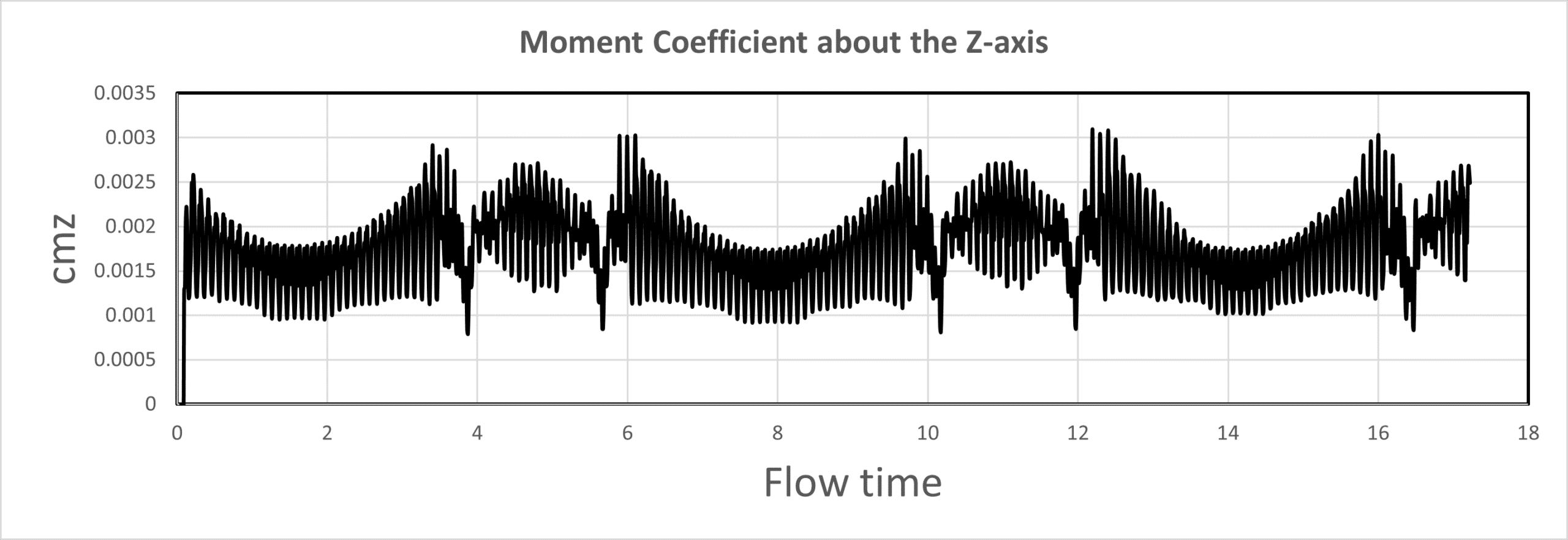
C_mz (Moment Coefficient about the Z-axis):

The equation y = -0.0029x + 0.0018 shows a negative relationship between CMz and the angle of attack. The slope of -0.0029 represents the yaw moment derivative (Cnr) about the z-axis, indicating that the quadcopter experiences a rolling moment as the angle of attack changes. The oscillations in CMz over the flow time and angle of attack suggest the presence of a roll-damping moment that affects the quadcopter’s roll stability.

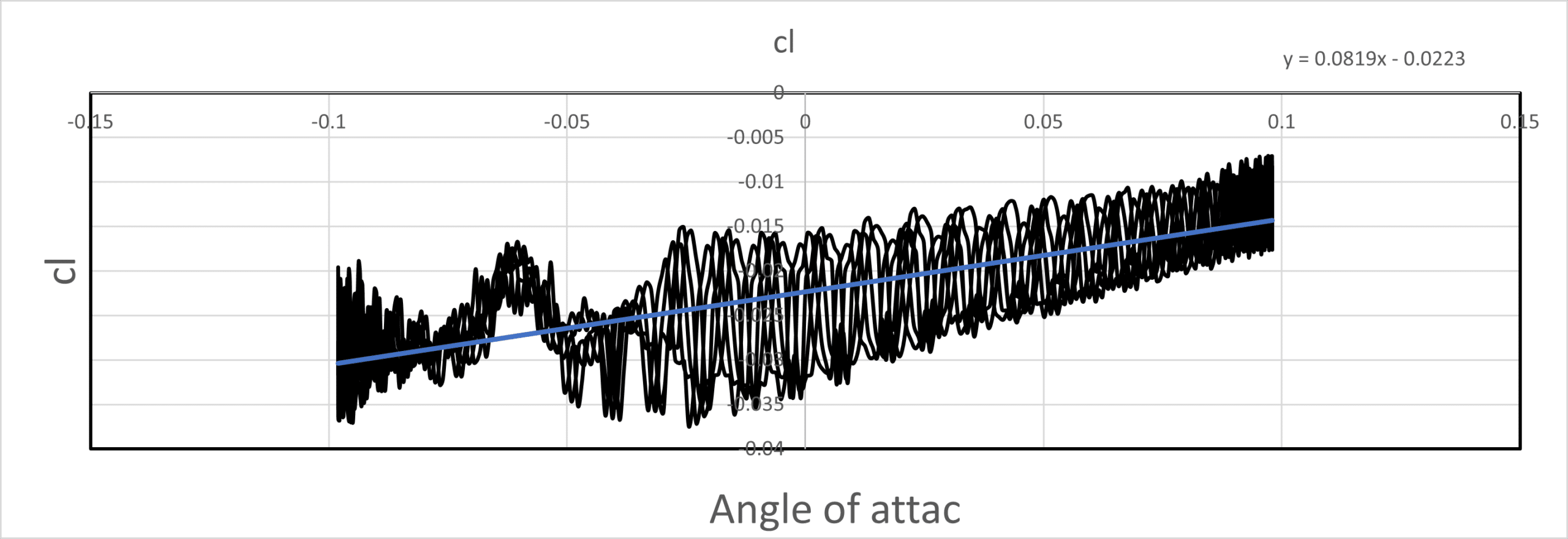
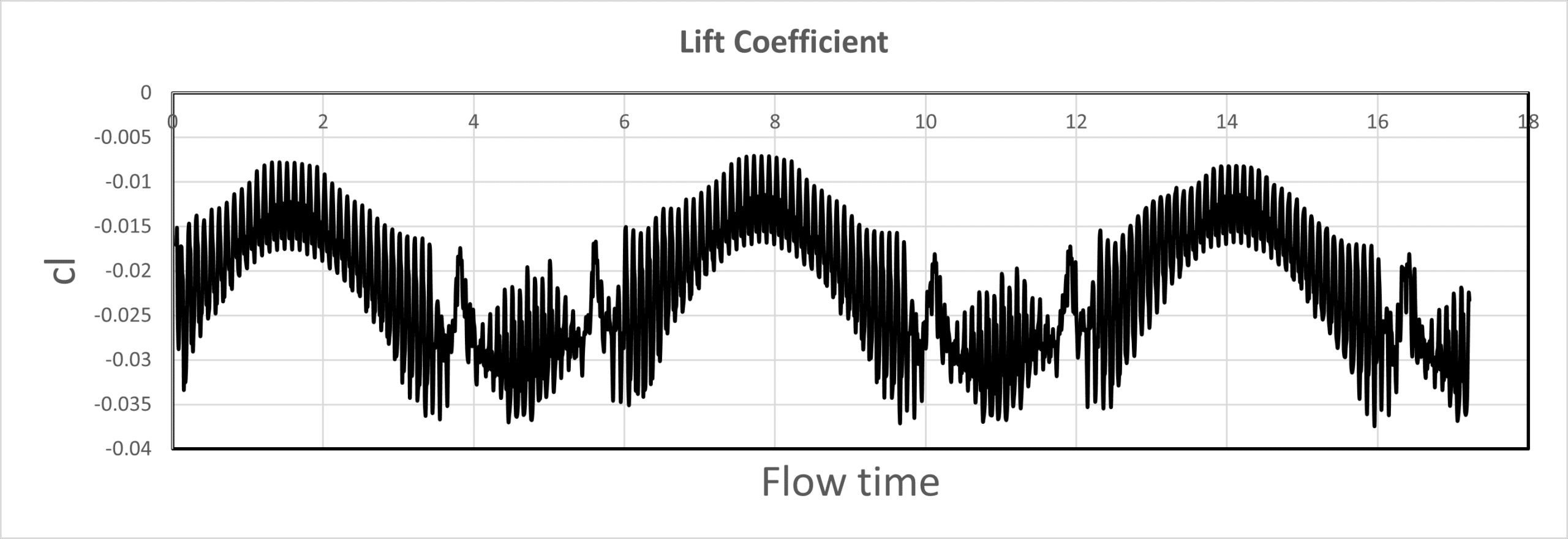
LIFT (Lift Coefficient):

The equation y = 0.0819x – 0.0223 shows a positive relationship between the lift coefficient and the angle of attack. The slope of 0.0819 represents the lift force derivative (CLα), indicating that the quadcopter generates lift force as the angle of attack increases. The periodic oscillations in the lift coefficient over the flow time and angle of attack suggest that the quadcopter experiences varying lift forces during its rotation.

The obtained dynamic stability derivatives provide insights into the quadcopter’s stability characteristics:

The positive lift force derivative (CLα) indicates that the quadcopter generates lift force as the angle of attack increases, which is essential for maintaining altitude.

The positive yaw moment derivative (Clp) suggests that the quadcopter experiences a yawing moment that affects its roll stability.

The positive pitch moment derivative (Cmq) indicates the presence of a pitching moment that influences the quadcopter’s pitch stability.

The negative roll moment derivative (Cnr) suggests that the quadcopter experiences a rolling moment that affects its yaw stability.

The periodic oscillations in the aerodynamic coefficients over the flow time and angle of attack indicate the presence of damping moments that contribute to the stability of the quadcopter’s motion.

To further enhance the understanding of the quadcopter’s dynamic stability, it would be beneficial to:

Validate the obtained stability derivatives against experimental data or theoretical predictions to ensure their accuracy.

Analyze the coupling between the aerodynamic coefficients and the motion variables to gain insights into the quadcopter’s dynamic stability behavior.

Investigate the influence of different flight conditions, such as forward speed and rotational rates, on the stability derivatives.

By leveraging the CFD simulation results and the dynamic stability derivatives, engineers can make informed design decisions and optimize the quadcopter’s stability and control characteristics for safe and efficient operation.