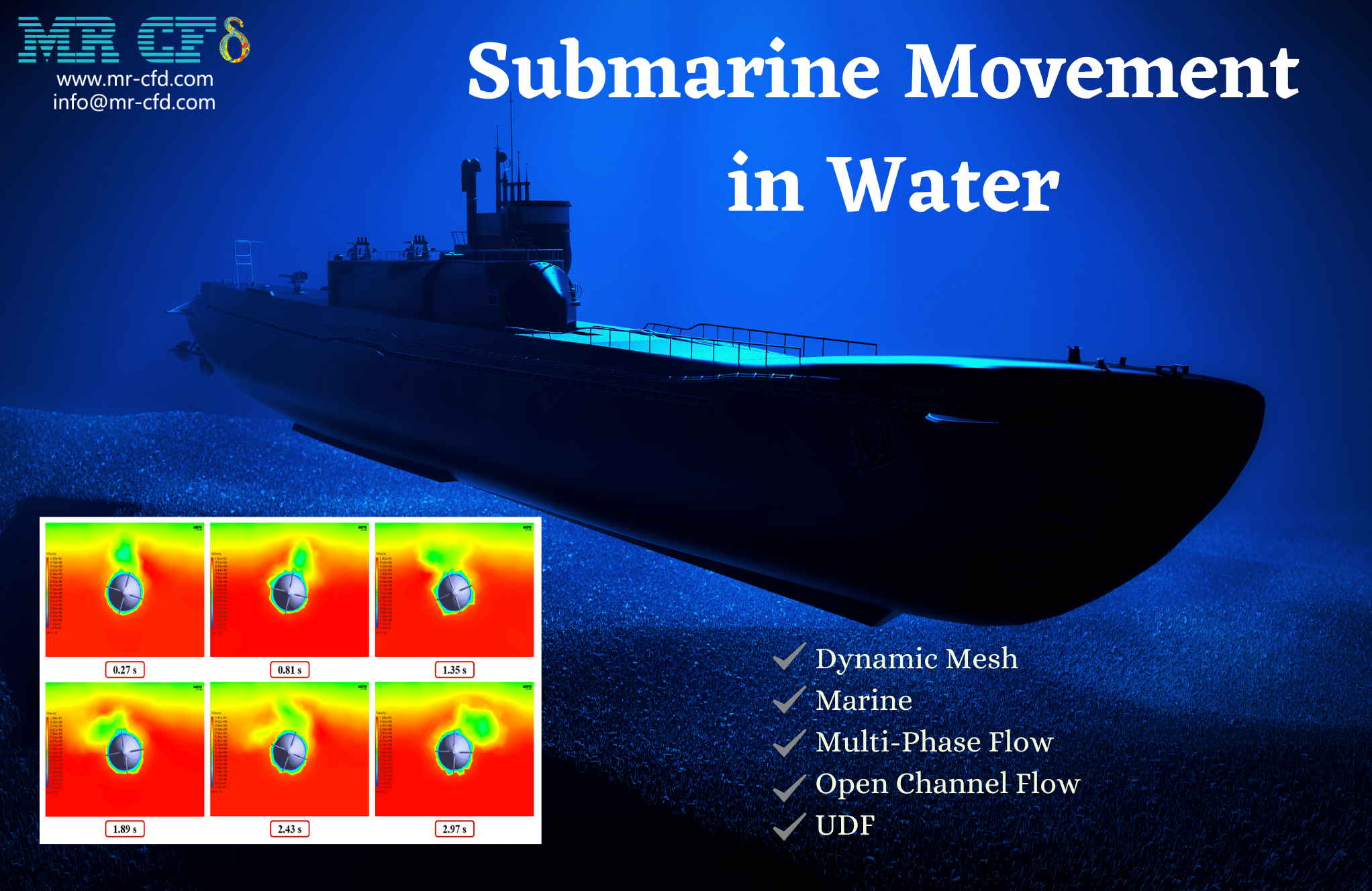
Self-Propelled Submarine Motion, Dynamic Mesh (6-DOF)

Description

The present problem simulates the motion of a self-propelled submarine floating on the water surface by dynamic mesh method using ANSYS Fluent software.

This product is the fourth chapter of the Dynamic Mesh Training Course.

In this simulation, a computational domain considering air and water with a certain level is designed; So that a self-propelled submarine is floating on the surface of the water.

We design the present model in three dimensions using AutoCAD, CATIA, and ICEM software. The horizontal length of the submarine is 16.25 m, and at its end, there are several impellers with a diameter of 0.825 m.

Around the submarine, we design a cylindrical computational area inside a cubic area as the total computational domain. We carry out the meshing using ICEM software.

The mesh type is hybrid (a combination of structured and unstructured); Thus, meshing in areas close to the submarine hull is unstructured and generally structured areas of the model. Also, the element number is equal to 2802219.

Self-Propelled Submarine Methodology

In such models, the location of the cells in the grid changes due to the displacement of their adjacent boundaries over time. Therefore, we benefit from the dynamic mesh model to define the instantaneous grid shift.

Initially, a self-propelled submarine was designed for this simulation, and three computational zones were created around the submarine. In determining dynamic mesh methods, smoothing and remeshing methods have been used.

Six degrees of freedom (six-DOF) have also been used to define the type of dynamic mesh behavior; This means that the model can move and relocate at six degrees. The properties of six degrees of freedom, including the mass and the moment in different directions for this model, are defined as a UDF.

To define areas with dynamic mesh, the body or walls of the submarine itself are defined as a Rigid Body. A small cylindrical area around the submarine is defined as a rigid body. And then, around this cylindrical region, a larger cubic area of ​​the Deforming type is defined.

This means that the submarine and a limited area around it act as a rigid and integrated body and can be moved in a transitional or rotational manner without any change in meshing.

It should be noted that in the section related to the Rigid Body, the spatial coordinates of the submarine center of gravity should be defined, as well as its position in the model. The submarine is defined as floating on the water’s surface.

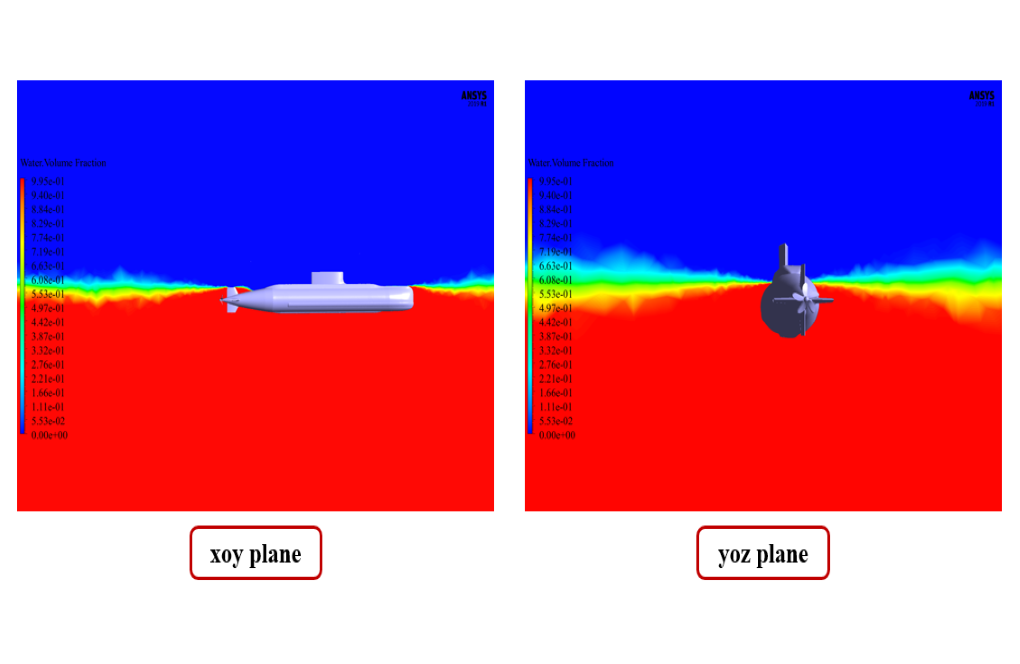
The volume of fluid (VOF) multiphase flow model should be used. So that in the upper part of the computational area, air and the lower part, water are defined. Both phases flow at a speed equal to 1.62 m/s in the horizontal direction (X-axis) and exit at a pressure equivalent to atmospheric pressure.

The open channel condition is used at the output to define the water level. It is assumed that the free water level at the outlet of the computational area is equal to 1.084824 m, and the height of the floor is equal to -100 m.

Due to the main nature of the model based on the use of dynamic mesh, the solver simulation should be defined as Transient. The present model performs the simulation process in 10 seconds with a time step size of 0.001 seconds.

Self-Propelled Submarine Conclusion

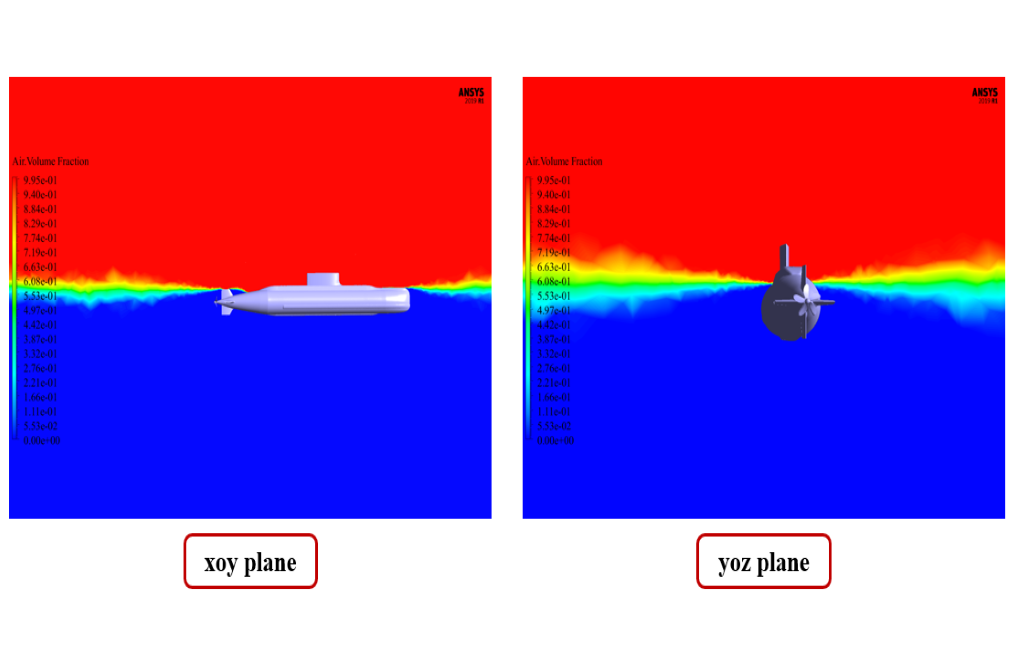
At the end of the solution process, we obtain two-dimensional contours related to the velocity and volume fraction of each air and water phase in the floating submarine areas.

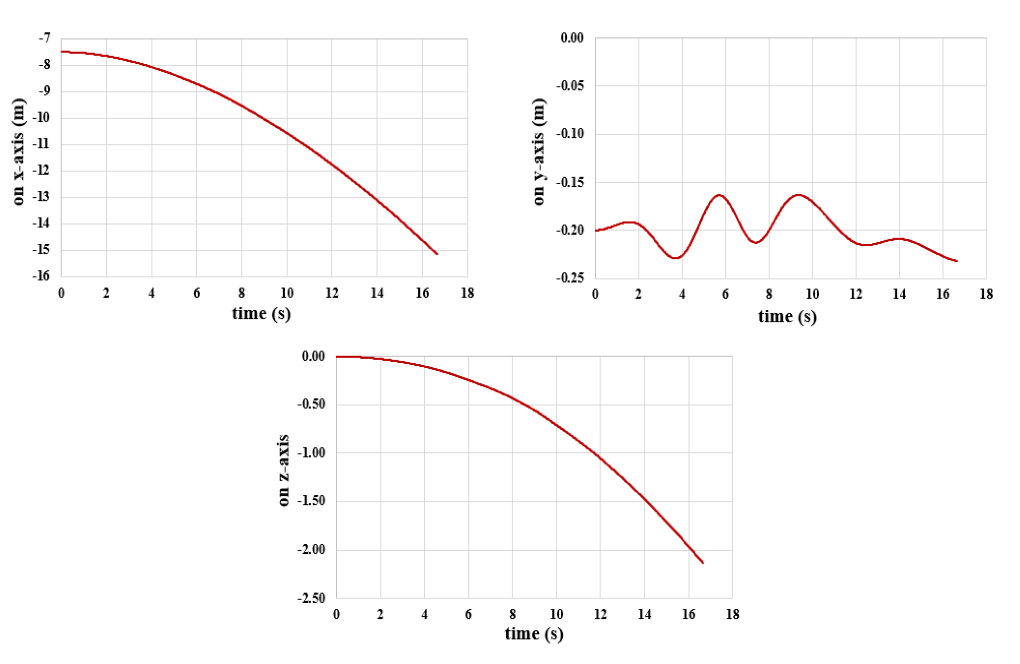
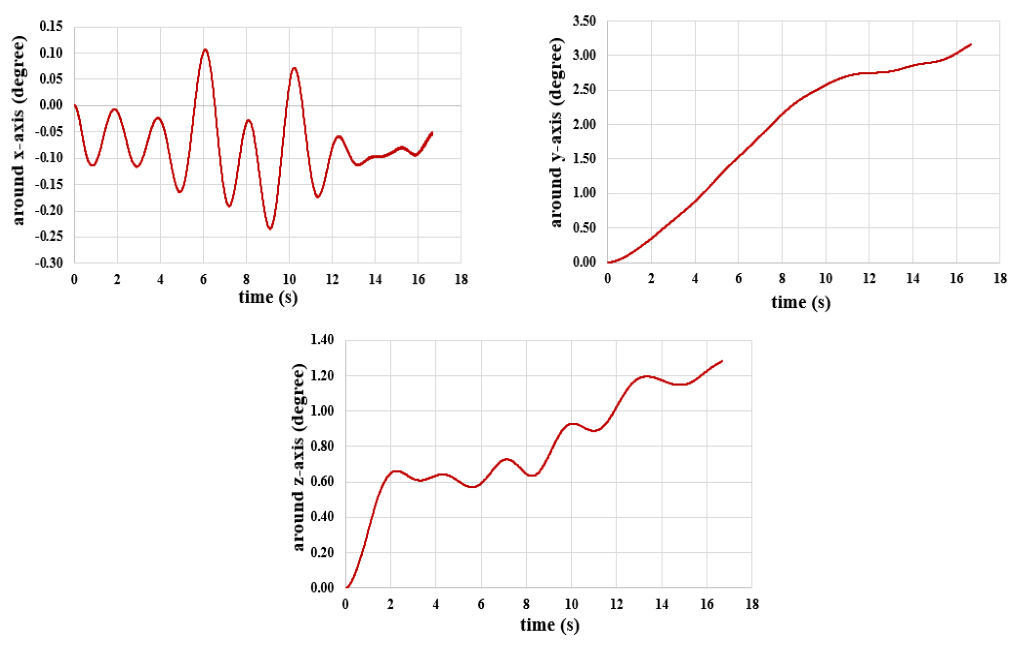
We present these contours in two planes, X-Y and Y-Z, and in the last second of the simulation process. Also, we show the diagram of the amount of submarine transitional and rotational movement in the direction of all three axes, X, Y, and Z.